- ПЛАСТИЧНОСТИ УСЛОВИЕ
- ПЛАСТИЧНОСТИ УСЛОВИЕ
-
(текучестиусловие) - соотношение матем. пластичности теории, определяющееграницу, отделяющую область пластического (точнее, упругопластического)состояния материала от области его упругого состояния. При выполпеиии П. <у. в материале начинают возникать остаточные деформации. П. у. записываетсяв виде
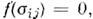где 
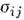-компоненты тензора напряжений. Для изотропного тела П. у. - ф-ция инвариантовтензора напряжений. Установление П. у. - одна из осн. задач эксперим. работ, <посвящённых феноменологич. теории пластичности. При эксперим. определенииП. у. изучается однородное напряжённое состояние (состояние, при к-ромнапряжения и деформации одинаковы во всех точках тела), к-рое реализуетсяв ср. части растягиваемых круглых или плоских образцов, а также при деформированиитонкостенных трубок, находящихся под действием растягивающей силы Р,внутр. давления р и крутящего момента М (рис. 1). В др. случаях(плоское деформиров. состояние, пространственное напряжённое состояниеи др.) П. у. подтверждается лишь косвенно при сравнении теоретич. и эксперим. <значений П. у., полученных при нагружении и разгрузке неоднородно напряжённыхпластич. тел.
Для металлов наиболее применимы П. у. <Треска (Н. Tresca, 1864) и Мизеса (R. Mises, 1913). Согласно П. у. Треска, <пластич. деформация в точке тела возникает, когда макс. касательное напряжение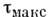
достигает нек-рого предельного значения 
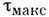= k= const. Поскольку 
равно одной из полуразностей гл. напряжений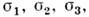 
то П. у. Треска записывается в виде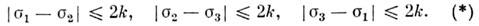 
Если за оси координат выбрать
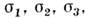то каждая точка этого пространства отвечает определённому напряжённомусостоянию точек тела. Все напряжённые состояния точек тела, удовлетворяющиенеравенствам (*), находятся в пространстве гл. напряжений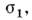 
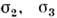внутри нек-рой шестигранной призмы, т. н. призмы Треска (рис. 2). Геом. <П. у. Треска утверждает, что пластич. деформации в точке тела возникнутв случае, если напряжённое состояние этой точки будет лежать в пространствегл. напряжении на призме Треска.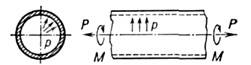
Рис. 1. Схема деформирования тонкостеннойтрубки.
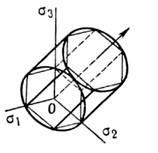
Рис. 2. Призма Треска и цилиндр Мизеса.
Согласно П. у. Мизеса, пластич. деформациивозникают, когда интенсивность касат. напряжений
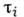достигает нек-рой пост. величины 
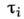= k= const. П. у. Мизеса записывается через главные напряженияв виде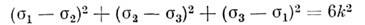 
и изображается в пространстве гл. напряженийцилиндром Мпзеса, описанным около призмы Треска.
Оба П. у. - Треска и Мизеса - дают малоотличающиеся результаты, т. к. их отношение заключено в близких пределах0,816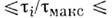
0,941. В конкретных случаях обычно пользуются тем из нпх, к-рое упрощаетматем. решение задачи. Различие между П. у. Треска и Мизеса может бытьнаглядно проиллюстрировано на примере плоского напряжённого состояния (одноиз гл. напряжений равно нулю), когда П. у. Треска и Мизеса изображаютсясоответственно шестиугольником и эллипсом (рис. 3).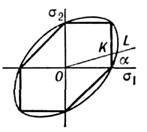
Рис. 3. Шестиугольник Треска и эллипс Мизесадля плоской задачи. При пропорциональном нагружении
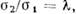
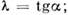напряжённое состояние изображается точками прямой OL; разница вусловиях пластичности Треска и Мизеса изображается отрезком KL.П. у. может быть рассмотрено в качествепластич. потенциала. В этом случае П. у. определяет, согласно ассоцииров. <закону пластич. течения (см. Пластичности теория), связь между компонентамиприращений деформации и напряжениями.
Лит.: Соколовский В. В., Теорияпластичности, 3 изд., М., 1969; Ильюшин А. А., Пластичность, ч. 1, М. -Л., 1948; Работнов Ю. Н., Механика деформируемого твердого тела, 2 изд.,М., 1988.
Д. Д. Ивлев.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
