- ОБОБЩЁННАЯ ФУНКЦИЯ
- ОБОБЩЁННАЯ ФУНКЦИЯ
-
- матем. понятие, <обобщающее классич. понятие ф-ции. Потребность в таком обобщении возникаетво многих техн., физ. и матем. задачах. Понятие О. ф. даёт возможностьвыразить в математически корректной форме такие идеализир. понятия, какплотность материальной точки, точечного заряда, точечного диполя, плотность(пространств.) простого или двойного слоя, интенсивность мгновенного источникаи т. д. С др. стороны, в понятии О. ф. находит отражение тот факт, чтореально нельзя измерить значение физ. величины в точке, а можно измерятьлишь её ср. значения в достаточно малых окрестностях данной точки. Т. <о.,О. ф. служат удобным и адекватным аппаратом для описания распределенийразл. физ. величин, поэтому О. ф. наз. также распределениями.
О. ф. были введены впервые в кон. 20-хгг. 20 в. П. Дираком (P.A.M. Dirac) в его исследованиях по квантовой механике. <Основы матем. теории О. ф. были заложены С. Л. Соболевым в 1936 при решениизадачи Коши для гпперболич. ур-ний, а в 50-х гг. Л. Шварц (L. Schwartz)дал систематич. изложение теории О. ф. и указал мн. применения. ТеорияО. ф. имеет многочисл. применения и вошла в обиход математиков, физикови инженеров.
Основные определения. Формально О. ф.f определяют как линейный непрерывный функционал над тем или иным векторнымпространством достаточно "хороших" (основных) ф-ций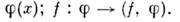 Важным примером основного пространства является пространство D(O )бесконечнодифференцируемых финитных в открытом множестве
Важным примером основного пространства является пространство D(O )бесконечнодифференцируемых финитных в открытом множестве 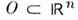 ф-ций
ф-ций 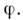 Наим. замкнутое множество, вне к-рого
Наим. замкнутое множество, вне к-рого 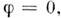 наз. носителем
наз. носителем 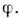 Последовательность
Последовательность 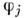 сходится к ф-ции
сходится к ф-ции 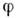 в D(О), если носители ф-ций
в D(О), если носители ф-ций 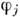 содержатсяв нек-ром ограниченном замкнутом подмножестве О и любая производнаяф-ций
содержатсяв нек-ром ограниченном замкнутом подмножестве О и любая производнаяф-ций 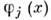 сходитсяпри
сходитсяпри 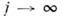 равномерно по х к соответствующей производной ф-ции
равномерно по х к соответствующей производной ф-ции 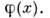
Примером основной ф-ции из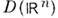 служит "шапочка"
служит "шапочка"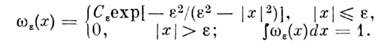
Соответствующее D(O )пространствоО. ф. обозначают D'(O);
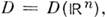
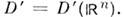 Сходимостьпоследовательности О. ф. из D'(0 )определяют как слабую сходимостьфункционалов в D'(О), т. е. fk - > 0,
Сходимостьпоследовательности О. ф. из D'(0 )определяют как слабую сходимостьфункционалов в D'(О), т. е. fk - > 0, в D'(O )означает, что
в D'(O )означает, что 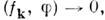
 для всех
для всех 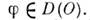
Для того чтобы линейный фунционал f на D(O )был О. ф. в О, т. е.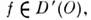 необходимо и достаточно, чтобы для любого открытого множества
необходимо и достаточно, чтобы для любого открытого множества 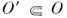 существовали числа К и т такие, что
существовали числа К и т такие, что 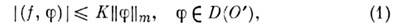
где
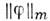 означает верх. грань модуля
означает верх. грань модуля 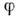 и её производных порядка
и её производных порядка 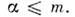
Если в неравенстве (1) целое число . независит от О', то О. ф. f имеет конечный порядок; наименьшеетакое т наз. порядком f в О. Т. о., в силу (1) всякаяО. ф. f из D'(O )имеет конечный порядок в любом
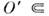 О.
О.Пространство D'(O) - полное: еслипоследовательность О. ф. fk, k =1, 2, ..., из D'(O )такова, <что для любой ф-ции
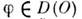 числовая последовательность
числовая последовательность 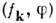 сходится, то функционал
сходится, то функционал 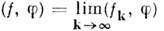 принадлежит D'(O).
принадлежит D'(O).
Простейшими примерами О. ф. являются функционалы, <порождаемые локально интегрируемыми в О ф-циями: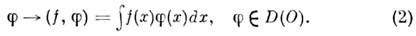
О. ф., определяемые локально интегрируемымив О ф-циямп f(x )по ф-ле (2), наз. регулярными О. ф. в О; остальныеО. ф. наз. сингулярными.
Примером сингулярной О. ф. в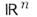 служит дельта-функция Дирака,
служит дельта-функция Дирака,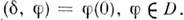 Она описывает плотность массы 1, сосредоточенной в точке х =0.При этом "шапочка"
Она описывает плотность массы 1, сосредоточенной в точке х =0.При этом "шапочка"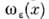 аппроксимирует
аппроксимирует 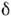 -функцию,
-функцию,
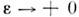 в D'. Пусть
в D'. Пусть 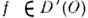 и
и 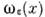 -"шапочка". Тогда ф-ция
-"шапочка". Тогда ф-ция 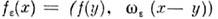 наз. регуляризацией О. ф. f и
наз. регуляризацией О. ф. f и 
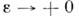 в D'(О). Более того, всякая f из D'(O )есть слабый пределф-ций из D(O). Последнее свойство иногда берут в качестве исходногодля определения О. ф., что вместе с теоремой о полноте пространства О. <ф. приводит к эквивалентному определению О. ф.
в D'(О). Более того, всякая f из D'(O )есть слабый пределф-ций из D(O). Последнее свойство иногда берут в качестве исходногодля определения О. ф., что вместе с теоремой о полноте пространства О. <ф. приводит к эквивалентному определению О. ф.
О. ф., вообще говоря, не имеют значенийв отд. точках. Тем не менее можно говорить о совпадении О. ф. с локальноинтегрируемой ф-цией на открытом множестве: О. ф. . из D'(O )совпадаетв О'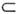 О слокальноинтегрируемой в О' ф-цией f0( х), если еёсужение на О' есть f0, т. е. в соответствии с(2)
О слокальноинтегрируемой в О' ф-цией f0( х), если еёсужение на О' есть f0, т. е. в соответствии с(2)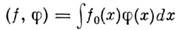
для всех
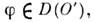 при этом считается f = f0(x),
при этом считается f = f0(x),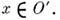 В частности, при f0
В частности, при f0 0 получается определение того, что О. ф. f обращается в нуль в О'. Множествоточек О, ни в какой окрестности к-рых О. ф. f не обращаетсяв нуль, наз. носителем О. ф. f и обозначается suppf. Еслиsupp
0 получается определение того, что О. ф. f обращается в нуль в О'. Множествоточек О, ни в какой окрестности к-рых О. ф. f не обращаетсяв нуль, наз. носителем О. ф. f и обозначается suppf. Еслиsupp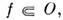 то О. <ф. / наз. финитной в О.
то О. <ф. / наз. финитной в О.
Справедлива теорема о кусочном склеиванииО. ф.: пусть в окрестности Uy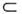 О каждойточки у задана О. ф. fy из D'(Uy), причёмэлементы f у согласованы, т. е. fy1 = fy2 в
О каждойточки у задана О. ф. fy из D'(Uy), причёмэлементы f у согласованы, т. е. fy1 = fy2 в 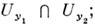 тогда существует О. ф. f из D'(О), совпадающая с fy в U у привсех у
тогда существует О. ф. f из D'(О), совпадающая с fy в U у привсех у 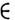 0.
0.
Напр., для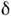 -функцииДирака: supp
-функцииДирака: supp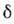 ={0}. О. ф.
={0}. О. ф.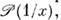 определяемая равенством
определяемая равенством 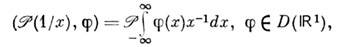
наз. главным значением интеграла отф-ции 1/ х;supp
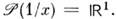 О. ф.
О. ф.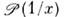 сингулярна в
сингулярна в 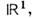 однако на открытом множестве х
однако на открытом множестве х 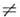 0она регулярна и совпадает с 1/х.
0она регулярна и совпадает с 1/х.Поверхностная
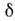 -функция. Пусть S - кусочно гладкая поверхность и
-функция. Пусть S - кусочно гладкая поверхность и 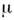 - непрерывная ф-ция на S. О. <ф.
- непрерывная ф-ция на S. О. <ф.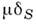 определяется равенством
определяется равенством 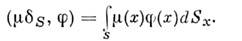
При этом
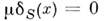 вне S,
вне S,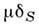 - сингулярная О. ф. Эта О. ф. описывает пространств. плотность масс илизарядов, сосредоточенных на поверхности S с поверхностной плотностью
- сингулярная О. ф. Эта О. ф. описывает пространств. плотность масс илизарядов, сосредоточенных на поверхности S с поверхностной плотностью 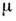 (плотность простого слоя).
(плотность простого слоя).
Линейные операции над О. ф. вводят какрасширение соответствующих операций над основными ф-циями.
Замена переменных. Пусть f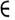 D'(O )и х= Ау+ b - линейное преобразование О на Oldet A
D'(O )и х= Ау+ b - линейное преобразование О на Oldet A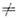 0. О. ф. f(Ay+ b )из D'(О' )определяют равенством
0. О. ф. f(Ay+ b )из D'(О' )определяют равенством 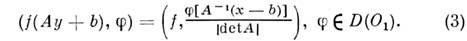
В частности, если

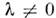 (.=
(.=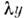 - подобие), то
- подобие), то 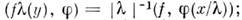 если А - I(х=у+b- сдвиг на b), то
если А - I(х=у+b- сдвиг на b), то 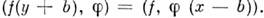 Ф-ла (3) позволяет определить трансляционно инвариантные, сферически симметричные, <центрально симметричные, однородные, периодические и т. д. О. ф.
Ф-ла (3) позволяет определить трансляционно инвариантные, сферически симметричные, <центрально симметричные, однородные, периодические и т. д. О. ф.
Пусть непрерывно дифференцируемая ф-ция а имеет только простые нули х 1, x2,... на оси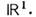 Ф-цию
Ф-цию 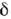 ( а(х) )определяютравенством
( а(х) )определяютравенством 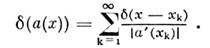
Напр.,
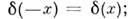
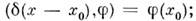
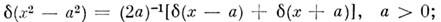
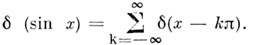
Произведение. Пусть f
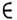 D'(0 )и
D'(0 )и 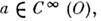 произведение а f = f а определяют равенством
произведение а f = f а определяют равенством 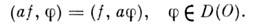
Оказывается, что af
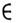 D'(0 )идля обычных ф-ций произведение а f совпадает с обычным умножениемф-ций f(x )и а(х). Напр.,
D'(0 )идля обычных ф-ций произведение а f совпадает с обычным умножениемф-ций f(x )и а(х). Напр.,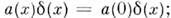
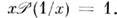
Однако эта операция произведения не допускаетраспространения на любые О. ф. так, чтобы она была ассоциативной и коммутативной. <В нек-рых классах О. ф. такое произведение можно определить, однако ономожет оказаться неоднозначным.
Дифференцирование. Пусть f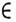 D'(O). Обобщённуюпроизводную О. ф. f
D'(O). Обобщённуюпроизводную О. ф. f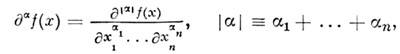 порядка
порядка 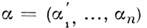 определяют равенством
определяют равенством 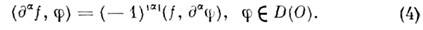
Т. к. операция
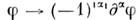 линейна и непрерывна, то функционал
линейна и непрерывна, то функционал 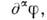 определяемый правой частью равенства (4), есть О. ф. из D'(O).
определяемый правой частью равенства (4), есть О. ф. из D'(O).
Имеют место след. свойства: операция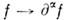 линейна и непрерывна, любая О. ф. из D'(O )бесконечно дифференцируема(в обобщённом смысле); дифференцирование не зависит от порядка; справедливаф-ла Лейбница для дифференцирования произведения а f, где
линейна и непрерывна, любая О. ф. из D'(O )бесконечно дифференцируема(в обобщённом смысле); дифференцирование не зависит от порядка; справедливаф-ла Лейбница для дифференцирования произведения а f, где 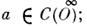 дифференцирование не увеличивает носителя; всякая О. ф. f из D'(О )вовсяком открытом множестве О'
дифференцирование не увеличивает носителя; всякая О. ф. f из D'(О )вовсяком открытом множестве О' О естьнек-рая производная от непрерывной ф-ции в О'; любое дифференц. <ур-пие Lu= f, f
О естьнек-рая производная от непрерывной ф-ции в О'; любое дифференц. <ур-пие Lu= f, f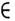 D'(О )спост. коэф. разрешимо в D'(O); любая О. ф. f порядка Nс носителем в точке 0 единств, образом представима в виде
D'(О )спост. коэф. разрешимо в D'(O); любая О. ф. f порядка Nс носителем в точке 0 единств, образом представима в виде 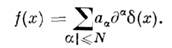
Напр.,
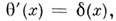 где
где 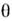 - ф-ция Хевисайда:
- ф-ция Хевисайда: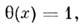 <<х>= 0;
<<х>= 0;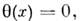 .<0;
.<0;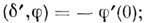
ф-ция -
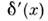 описывает плотность зарядов, соответствующую диполю момента, равного +1в точке х= О и ориентированного вдоль положительного направленияоси х.
описывает плотность зарядов, соответствующую диполю момента, равного +1в точке х= О и ориентированного вдоль положительного направленияоси х.Обобщением
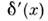 является нормальная производная от плотности простого слоя на ориентируемойповерхности S:
является нормальная производная от плотности простого слоя на ориентируемойповерхности S: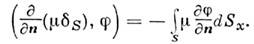
О. ф. -
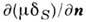 описывает пространств. плотность зарядов, соответствующих распределениюдиполей на поверхности S с поверхностной плотностью момента
описывает пространств. плотность зарядов, соответствующих распределениюдиполей на поверхности S с поверхностной плотностью момента 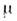 и ориентированных вдоль заданного направления нормали n на . (плотностьдвойного слоя).
и ориентированных вдоль заданного направления нормали n на . (плотностьдвойного слоя).
Общее решение ур-ния хи = О в классе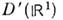 есть и(х) =
есть и(х) =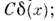
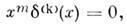 k = 0,1, ...,m - 1. Тригонометрич. ряд
k = 0,1, ...,m - 1. Тригонометрич. ряд 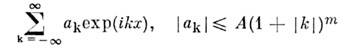
сходится в D', и его можно дифференцироватьв D' почленно любое конечное число раз;
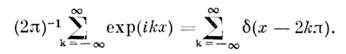
Прямое произведение. Пусть f(x )и g(y )-локально интегрируемые ф-ции в пространствах
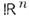 и
и 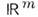 соответственно. <Ф-ция f(x )х g(y) локально интегрируема в
соответственно. <Ф-ция f(x )х g(y) локально интегрируема в 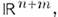 она определяет регулярную О. ф.
она определяет регулярную О. ф.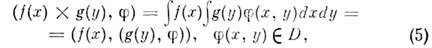
наз. прямым произведением f и g. Ф-ла(5) служит основой для определения прямого произведения О. ф.f(x )из
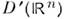 и g(y )из
и g(y )из 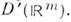 Прямое произведение коммутативно и ассоциативно. Напр.,
Прямое произведение коммутативно и ассоциативно. Напр.,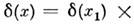
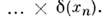
Свёртка. Если f(x )и g(x )локальноинтегрируемы в
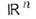 и ф-ция
и ф-ция 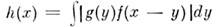 также локально интегрируема в
также локально интегрируема в 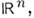 то свёрткой f * g наз. ф-ция
то свёрткой f * g наз. ф-ция 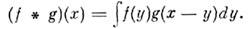
Эта ф-ция локально интегрируема в
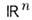 и определяет регулярную О. ф.:
и определяет регулярную О. ф.: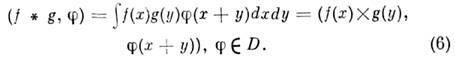
Свёртка заведомо существует, если однаиз ф-ций f или g финитна. Если свёртка существует, то онакоммутативна: f * g = g * f; справедливы ф-лы дифференцированиясвёртки:
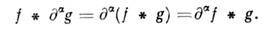
Если учесть, что
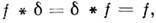 получим
получим 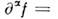
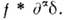
Свёртка, вообще говоря, не ассоциативна. <Однако если рассмотреть, напр., совокупность D'+ О. ф. из D'(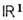 ),обращающихся в нуль при х< 0, то их свёртка существует и ассоциативна.
),обращающихся в нуль при х< 0, то их свёртка существует и ассоциативна.
О. ф.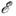 из D' наз. фундаментальным решением (ф-цией точечного источника)дифференц. оператора L(д )с пост. коэффициентами, если она удовлетворяетур-нию
из D' наз. фундаментальным решением (ф-цией точечного источника)дифференц. оператора L(д )с пост. коэффициентами, если она удовлетворяетур-нию 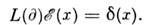
Зная фундам. решение
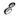 оператора L(д), можно построить решение ур-ния L(d)u = f для тех f из D', для к-рых свёртка f *
оператора L(д), можно построить решение ур-ния L(d)u = f для тех f из D', для к-рых свёртка f *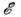 существует, <и это решение даётся ф-лой
существует, <и это решение даётся ф-лой 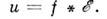 Напр., для ур-ния
Напр., для ур-ния 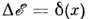
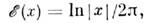 п= 2;
п= 2;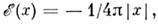 п = 3
п = 3(см. также Грина функция).
Преобразование Фурье определяютдля класса О. ф. S' = S'(
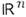 )медленного роста. Пространство основных ф-ций S= S(
)медленного роста. Пространство основных ф-ций S= S(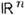 )состоитиз ф-ций, убывающих на бесконечности вместе со всеми производными быстреелюбой степени | х | -1. Норма в S задаётся выражением
)состоитиз ф-ций, убывающих на бесконечности вместе со всеми производными быстреелюбой степени | х | -1. Норма в S задаётся выражением 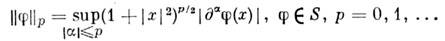
Локально интегрируемые в
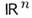 ф-ции медленного роста содержатся в S', определяя по ф-ле (2) регулярныефункционалы на S. Всякая О. ф. из S' есть нек-рая производнаяот непрерывной ф-ции медленного роста и, стало быть, имеет конечный порядокв
ф-ции медленного роста содержатся в S', определяя по ф-ле (2) регулярныефункционалы на S. Всякая О. ф. из S' есть нек-рая производнаяот непрерывной ф-ции медленного роста и, стало быть, имеет конечный порядокв 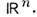
Преобразование Фурье .[f]О. <ф. f из S' определяется равенством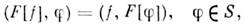
где
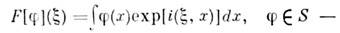 классич. преобразование Фурье. Обратная операция к F:
классич. преобразование Фурье. Обратная операция к F: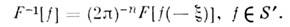
Основные ф-лы для f
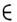 S':
S':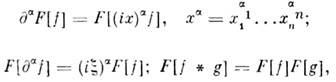
если g финитна. Если О. ф.f - периодическаяс периодом Т =( Т1, ..., Т п), Tjf
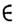 S' иеё можно разложить в тригонометрич. ряд
S' иеё можно разложить в тригонометрич. ряд 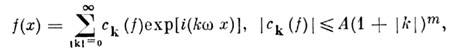
сходящийся к f в S'; здесь
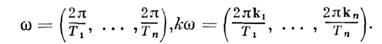
Напр.,
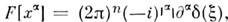 в частности F[1]=
в частности F[1]=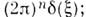
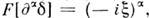 в частности
в частности 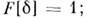
Преобразование Лапласа в одномерном случае.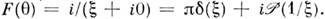 Пусть S'+ - пересечение множеств S' и D'+, тогда множество О. ф. из D'+, таких, что
Пусть S'+ - пересечение множеств S' и D'+, тогда множество О. ф. из D'+, таких, что 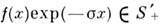 при всех
при всех 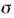 а, обозначают D'+(a). Если f и
а, обозначают D'+(a). Если f и 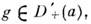 то
то 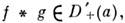 причём (f * g)exp( -
причём (f * g)exp( -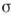 х)=/ехр( -
х)=/ехр( -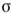 х)*gexp ( -
х)*gexp ( -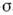 х),
х),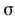 а.
а.
Пусть f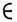 D'+ (a), тогда преобразование Лапласа f есть
D'+ (a), тогда преобразование Лапласа f есть 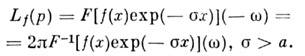
Lf (p) - аналитич. <ф-ция в полуплоскости
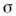 а. Ф-цию f(x )наз. оригиналом, ф-цию Lf (p)- изображением, между ними имеется взаимно однозначное соответствие f(x)<->Lf(p),
а. Ф-цию f(x )наз. оригиналом, ф-цию Lf (p)- изображением, между ними имеется взаимно однозначное соответствие f(x)<->Lf(p),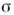 Обратное преобразование определяют равенством
Обратное преобразование определяют равенством 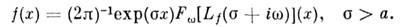
Справедливы след. ф-лы:
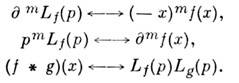
Напр.,
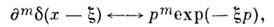
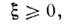 р- любое, m = 0,1,...
р- любое, m = 0,1,...Лит.: Гельфанд И. М., Шилов Г. Е.,Обобщенные функции, в. 1 - 3, М., 1958; Дирак П. А. М., Принципы квантовоймеханики, пер. с англ., 2 изд., М., 1979; Шварц Л., Математические методыдля физических наук, пер. с франц., М., 1965; Владимиров В. С., Уравненияматематической физики, 5 изд., М., 1988; его ж е, Обобщенные функции сматематической физике 2 изд., М., 1979; Антосик П., Микусинский Я. СикорскийР., Теория обобщенных функций. Секвенциальный подход, пер. с англ., М.,1976; Рихтмайер Р. Принципы современной математической физики, пер. с англ. <т. 1, М., 1982; Боголюбов Н. Н., Логунов А. А. Оксак А. И., Тодоров И. Т., Общиепринципы квантовой теории поля, М., 1987.
В. С. Владимиров.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
