- НЕУПРУГОЕ РАССЕЯНИЕ НЕЙТРОНОВ
- НЕУПРУГОЕ РАССЕЯНИЕ НЕЙТРОНОВ
-
- методисследования атомной динамики вещества (преим. в твёрдых телах и жидкостях).Изменение энергии нейтрона
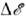 при неупругом рассеянии и зависимость
при неупругом рассеянии и зависимость 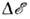 отпереданного импульса несёт информацию о спектре возбуждений вещества. Н. <р. н. на ядрах (см. Нейтронография )применяется для изучения элементарныхвозбуждений ( квазичастиц), связанных с трансляц., колебат. и вращат. <степенями свободы атомов и молекул. Магн. Н. р. н. позволяет исследоватьвозбуждения, возникающие при изменении спиновых и (или) орбитальных состоянийэлектронов. Когерентная составляющая Н. р. н. даёт информацию о коллективныхвозбуждениях частиц (фопонах, магнонах и т. д.), а некогерентная - о возбужденияхиндивидуальных частиц (спектральной плотности их колебаний, диффузии ит. д.).
отпереданного импульса несёт информацию о спектре возбуждений вещества. Н. <р. н. на ядрах (см. Нейтронография )применяется для изучения элементарныхвозбуждений ( квазичастиц), связанных с трансляц., колебат. и вращат. <степенями свободы атомов и молекул. Магн. Н. р. н. позволяет исследоватьвозбуждения, возникающие при изменении спиновых и (или) орбитальных состоянийэлектронов. Когерентная составляющая Н. р. н. даёт информацию о коллективныхвозбуждениях частиц (фопонах, магнонах и т. д.), а некогерентная - о возбужденияхиндивидуальных частиц (спектральной плотности их колебаний, диффузии ит. д.).Теоретическое описание. Рассеяниенейтронов в веществе принято описывать сечением рассеяния о, отнесённымк элементу телесного угла
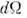 иинтервалу рассеянных энергий нейтронов
иинтервалу рассеянных энергий нейтронов 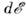 .Рассеяние нейтронов представляется в виде суммы когерентной и некогерентнойсоставляющих, первая из к-рых имеет интерференц. природу, а вторая определяетсясуммой сечений рассеяний от отд. частиц.
.Рассеяние нейтронов представляется в виде суммы когерентной и некогерентнойсоставляющих, первая из к-рых имеет интерференц. природу, а вторая определяетсясуммой сечений рассеяний от отд. частиц.
Дифференц. сечение когерентного рассеянияна одну частицу для системы из частиц одного сорта может быть представленов виде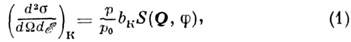
где р0 и р - импульсыпадающего и рассеянного нейтронов с энергиями
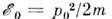 и
и 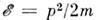 ( т- масса нейтрона);
( т- масса нейтрона);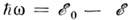 и
и 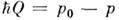 - изменениеэнергии и импульса нейтрона при рассеянии; b к- когерентнаяамплитуда рассеяния (значения b к табулированы). Когерентнаяф-ция рассеяния
- изменениеэнергии и импульса нейтрона при рассеянии; b к- когерентнаяамплитуда рассеяния (значения b к табулированы). Когерентнаяф-ция рассеяния 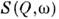 определяетсятолько свойствами системы:
определяетсятолько свойствами системы: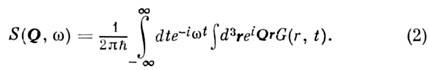
Здесь G(r,t) - парная корреляционнаяфункция, описывающая пространственно-временную корреляцию в расположениичастиц системы:
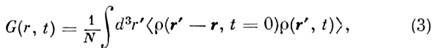
где
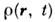 - плотность частиц в точке r пространства в момент времени t,а среднее
- плотность частиц в точке r пространства в момент времени t,а среднее 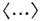 вычисляетсяпо равновесному состоянию системы частиц. Усреднённое по времени значениепарной корреляц. ф-ции
вычисляетсяпо равновесному состоянию системы частиц. Усреднённое по времени значениепарной корреляц. ф-ции 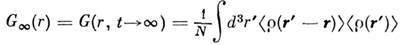
определяет в (2) упругое рассеяние, происходящеебез изменения энергии нейтронов, ,
 Неупругое рассеяние в (2) определяется разностью G'(r,t) =
Неупругое рассеяние в (2) определяется разностью G'(r,t) = зависящей лишь от флуктуации плотности частиц,
зависящей лишь от флуктуации плотности частиц,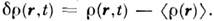 Т. о., когерентное Н. р. н. определяется динамикой флуктуации плотностичастиц вещества и поэтому связано с коллективными возбуждениями системы.
Т. о., когерентное Н. р. н. определяется динамикой флуктуации плотностичастиц вещества и поэтому связано с коллективными возбуждениями системы.Дифференц. сечение некогерентного рассеянияописывается ф-лой
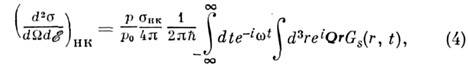
где
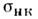 - сечение некогерентного рассеяния для частиц данного сорта (
- сечение некогерентного рассеяния для частиц данного сорта (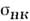 табулированы).Автокорреляц. ф-ция
табулированы).Автокорреляц. ф-ция 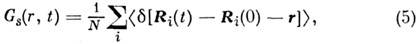
где Ri(t) - координата i -ичастицы в момент времени t. Ф-ция Gs(r,t )описываетвременную корреляцию в положении одной и той же частицы и поэтому несётинформацию о динамике (колебаниях, диффузии и т. д.) отд. частиц.
Н. р. н. в кристаллах. Наиб. успешнометод Н. р. н. используется при исследовании колебаний кристаллическойрешётки. Он позволяет определить фононные дисперсионные кривые и плотностьфононных состояний. Кристаллы обладают трансляц. симметрией, и поэтомумалые колебания атомов в них характеризуются определёнными значениями волновоговектора q, характеризующего пространств. когерентность смещенийатомов решётки. В результате этого зависимость сечения когерентного (однофононного)рассеяния нейтронов от их энергии содержит резко выраженные пики, положениек-рых определяется законами сохранения энергии
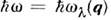 и импульса
и импульса 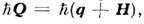 где
где 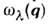 -частота колебаний ветви
-частота колебаний ветви 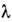 с волновым вектором q, приведённым к первой зоне Бриллюэна с помощьювыбора вектора обратной решётки Н.
с волновым вектором q, приведённым к первой зоне Бриллюэна с помощьювыбора вектора обратной решётки Н.
Для моноатомной решётки ф-ция однофононногокогерентного рассеяния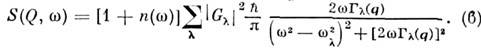
Здесь
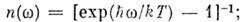 т. н. структурная амплитуда
т. н. структурная амплитуда 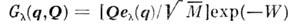 определяетзависимость интенсивности рассеяния от величины передаваемого импульса Q и его ориентации относительно вектора поляризации
определяетзависимость интенсивности рассеяния от величины передаваемого импульса Q и его ориентации относительно вектора поляризации 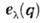 исследуемогофонона ( М - массы атомов, W(Q) - тепловой Дебая- Уоллера фактор). Спектральная интенсивность когерентного Н. р. н. <определяется вторым сомножителем в (6), где
исследуемогофонона ( М - массы атомов, W(Q) - тепловой Дебая- Уоллера фактор). Спектральная интенсивность когерентного Н. р. н. <определяется вторым сомножителем в (6), где 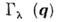 - затухание (величина, обратная времени жизни) фонопа. Для слабозатухающихфононов
- затухание (величина, обратная времени жизни) фонопа. Для слабозатухающихфононов 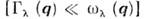 интенсивность рассеяния имеет два острых максимума при
интенсивность рассеяния имеет два острых максимума при 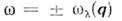 с полушириной пиков
с полушириной пиков 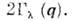 Температурная зависимость Н. р. н. с возбуждением фонопа в кристалле
Температурная зависимость Н. р. н. с возбуждением фонопа в кристалле 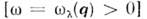 или поглощением его
или поглощением его 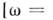
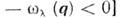 определяетсямножителями
определяетсямножителями 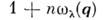 или
или 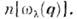
В экспериментах обычно измеряется зависимостьсечения рассеяния от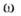 приразл. значениях вектора Q. По положению её максимумов и поих ширине с помощью обратного преобразования Фурье находится зависимостьчастоты фононов
приразл. значениях вектора Q. По положению её максимумов и поих ширине с помощью обратного преобразования Фурье находится зависимостьчастоты фононов 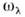 и их затухания
и их затухания 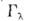 отволнового вектора q для каждой ветви
отволнового вектора q для каждой ветви 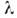 колебаний(рис. 1).
колебаний(рис. 1).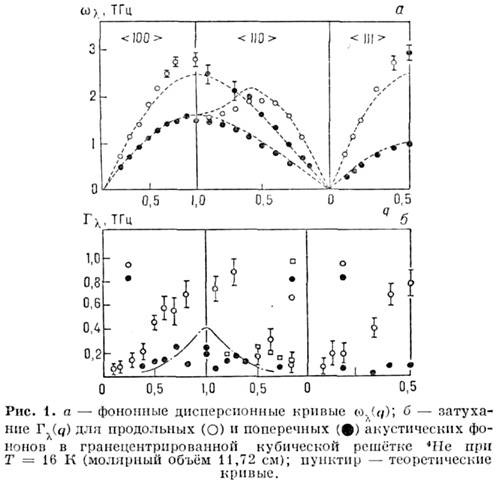
Н. р. н. даёт информацию о структурныхфазовых переходах 2-го рода в кристаллах, в т. ч. сегнетоэлектрических. <В частности, удаётся исследовать поведение т. н. критической "мягкой" модыколебаний, частота к-рой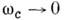 при Т-> Т С (Т С - темп-pa фазовогоперехода), а вектор поляризации описывает статистич. волну смещений атомовс волновым вектором qc, "замерзающую" при Т< Т с. Сечение рассеяния в этом случае обычно имеет одинквазиуиругпй пик при
при Т-> Т С (Т С - темп-pa фазовогоперехода), а вектор поляризации описывает статистич. волну смещений атомовс волновым вектором qc, "замерзающую" при Т< Т с. Сечение рассеяния в этом случае обычно имеет одинквазиуиругпй пик при 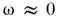 и q= qc, полная интенсивность к-рого растёт как
и q= qc, полная интенсивность к-рого растёт как 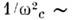
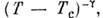 а ширина
а ширина 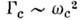 уменьшается как
уменьшается как 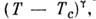 где
где 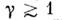 наз. крптич. индексом (см. Критические явления). Н. р. н. при .-> Т с отражает появление в кристалле упорядоченных областейновой фазы, время жизни к-рых
наз. крптич. индексом (см. Критические явления). Н. р. н. при .-> Т с отражает появление в кристалле упорядоченных областейновой фазы, время жизни к-рых 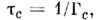 и размеры неограниченно возрастают при Т- с.
и размеры неограниченно возрастают при Т- с.
Некогерентное Н. р. н. происходит на отд. <атомах независимо и поэтому волновой вектор Q не фиксируется. <В результате этого сечение некогерентиого рассеяния определяется лишь закономсохранения энергии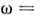
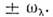 Поэтому оно имеет вид плавной ф-цин частоты
Поэтому оно имеет вид плавной ф-цин частоты 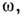 характеризующей плотность фононных состояний
характеризующей плотность фононных состояний 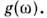
Для моноатомной решётки сечение некогерентногоН. р. н. может быть представлено в виде: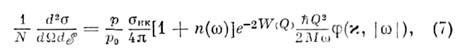
где
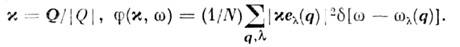
Для кубич. решётки
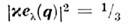 и ф-ция
и ф-ция 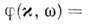
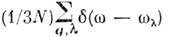 определяют плотность фононных состояний.
определяют плотность фононных состояний.
Некогерентное Н. р. н. часто используетсядля исследования динамики решётки водородсодержащнх кристаллов, т. к. вэтом случае осн. вклад в сечение рассеяния дают протоны (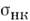 велико, М протона мала). Напр., в зависимости плотности фононныхсостояний ср от энергии фоионов
велико, М протона мала). Напр., в зависимости плотности фононныхсостояний ср от энергии фоионов 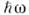 для поликристаллич. CsHS04 пики а, б, в обусловлены рассеяниемна протонах (рис. 2). При Т =414 К этот кристалл испытывает структурныйфазовый переход в состояние с высокой ионной проводимостью (см. Ионныесуперпроводники), к-рый сопровождается разупорядочением протонов врешётке. Рис. 2 показывает, что это приводит к изменению спектра фононныхчастот.
для поликристаллич. CsHS04 пики а, б, в обусловлены рассеяниемна протонах (рис. 2). При Т =414 К этот кристалл испытывает структурныйфазовый переход в состояние с высокой ионной проводимостью (см. Ионныесуперпроводники), к-рый сопровождается разупорядочением протонов врешётке. Рис. 2 показывает, что это приводит к изменению спектра фононныхчастот.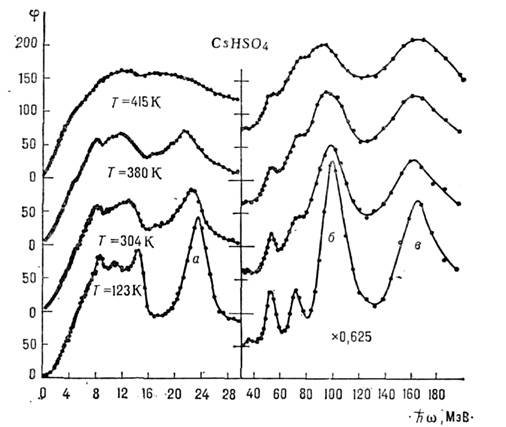
Рис. 2. Взвешенная плотность фононных состоянийф в зависимости от энергии фононов при различных температурах.
С помощью некогерентного рассеяния изучаютсятакже молекулярные вращения, диффузия протонов в металлах и т. д. Применениет. н. метода изотопич. контраста, состоящего в замене протона на дейтрон, <позволяет исследовать динамику отд. частей сложных молекул и получать информациюо характере хим. связи в молекулах.
И. р. н. в жидкостях. В отличиеот фононов в кристаллах, коллективные возбуждения в жидкости (флуктуацииплотности) ввиду отсутствия дальнего порядка и диффузии частиц быстро затухают(см. Дальний и ближний порядок). Поэтому
 в жидкости не имеет ярко выраженных пиков при
в жидкости не имеет ярко выраженных пиков при 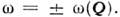 Обычно проводят теоретич. расчёт ф-ции
Обычно проводят теоретич. расчёт ф-ции 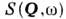 для определённой модели коллективных возбуждений и, сопоставляя её с экспериментальноизмеренной, находят параметры модели.
для определённой модели коллективных возбуждений и, сопоставляя её с экспериментальноизмеренной, находят параметры модели.
Наиб. изучены коллективные возбужденияв моноатомных жидкостях, как квантовых (4 Не, 3 Не),так и классических (Ne, Ar, Rb, Na). Напр., в сверхтекучем 4 Неблагодаря наличию дальнего порядка удалось наблюдать коллективные возбужденияв области импульсов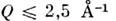 (рис. 3; см. Сверхтекучесть).
(рис. 3; см. Сверхтекучесть).
Некогерентное Н. р. н. в жидкости позволяетизучать характер диффузии частиц и их колебат. спектр.
Для анализа диффузии частиц в классич. <жидкостях обычно используется гауссовское приближение для автокорреляц. <ф-ции Gs(r, t):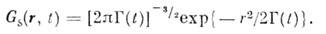
В этом приближении динамика частицы полностьюописывается т. п. ширинной ф-цией T(t), имеющей смысл среднего квадратичногосмещения частицы за время t:
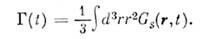
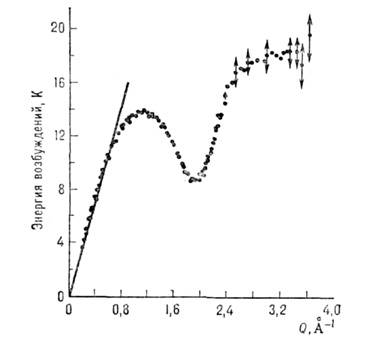
Рис. 3. Зависимость энергии коллективныхвозбуждений
 от волнового вектора Q в сверхтекучем гелии при Т= 1 ,1К.
от волнового вектора Q в сверхтекучем гелии при Т= 1 ,1К.Исследования с помощью Н. р. н. показываютсложный характер зависимости Г(t). В течение малых времён частицы движутсякак в идеальном газе:
 t2kT/M,а на протяжении больших времён выполняется классич. закон диффузии:
t2kT/M,а на протяжении больших времён выполняется классич. закон диффузии: где D - коэф. диффузии.
где D - коэф. диффузии.
Некогерентное Н. р. н. используется такжедля изучения колебат. и вращат. спектров молекул в жидкостях и плотныхгазах (напр., в Н 20).
Магнитное неупругое рассеяние. Магн. рассеяниенейтронов обусловлено взаимодействием магн. момента нейтрона с магн. моментамиэлектронных оболочек атомов, молекул, электронов проводимости в металлахи т. д. (см. Магнитная нейтронография]. Неупругое магн. рассеяниесвязано с рассеянием нейтронов на флуктуациях спиновой плотности, т. е. <с коллективными возбуждениями спиновой системы. Это - спиновые волны, (магноны)в магнитоупорядоченных средах, флуктуации намагниченности вблизи магн. <фазовых переходов, возбуждения индивидуальных спинов (парамагн. рассеяние)или полных моментов f -электронов при переходах между уровнями, обусловленнымивзаимодействием с внутрикристаллич. электрич. полем.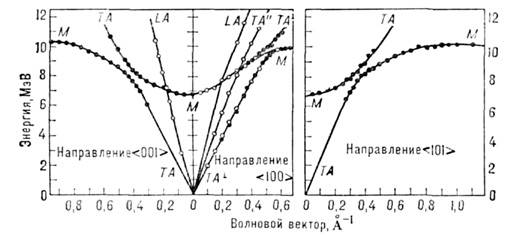
Рис. 4. Фононные и магнонная дисперсионныекривые в антнферромагнетике FeF2 при Т= 4,2 К; ТА -поперечный, LA - продольные акустические фононы, М - магноны.
Наиб. полно изучены одномагнонное рассеяниепри низких темп-pax в ферро- и антиферромагиетиках и рассеяние вблизи магн. <фазовых переходов. Одномагнонное рассеяние, как и однофононное, позволяетопределить частоту
 и затухание Г(q) магнона, величины магн. моментов магн. подрешёток. <Рассеяние при темп-ре Т- > Т с (критич. темп-pa)даёт возможность исследовать поведение критич. моды флуктуации спиновойплотности, "замораживание" к-рой определяет тип магн. дальнего порядкапри Т < Т с (см. Спиновой плотности волны).
и затухание Г(q) магнона, величины магн. моментов магн. подрешёток. <Рассеяние при темп-ре Т- > Т с (критич. темп-pa)даёт возможность исследовать поведение критич. моды флуктуации спиновойплотности, "замораживание" к-рой определяет тип магн. дальнего порядкапри Т < Т с (см. Спиновой плотности волны).
Взаимодействие спинов с фопонами можетпривести к появлению смешанных магнон-фононных возбуждений и интерференцииядерного и магн. рассеяния. Исследование Н. р. п. в области гибридизациимагнопа и фонола позволяет по величине расщепления оценить параметры спин-решёточноговзаимодействия (рис. 4).Лит.: Г уревич И. И., Тарасов Л. <В., Физика нейтронов низких энергий, М., 1965; Woods A. D. В., Соw1еуR. A., Structure and excitation of liquid helium, "Repts Progr. Phys.",1973, v. 36, p. 1135; Динамические свойства твердых тел и жидкостей. Исследованиеметодом рассеяния нейтронов, пер. с англ., М., 1980; Изюмов Ю. А., ЧерноплековП. А., Нейтронная спектроскопия, М., 1983; Аксенов В. Л., Планида Н. М.,Стаменкович С., Рассеяние нейтронов сегнетоилектриками, М., 1984; УиндзорК., Рассеяние нейтронов от импульсных источников, пер. с англ., М., 1985.
Н. М. Плакида.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
