МУЛЬТИПОЛИ

МУЛЬТИПОЛИ

(от лат. multum - много и греч. polos - полюс) - определённые конфигурации точечных источников (зарядов). Простейшими примерами M. служат: точечный заряд - M. нулевого порядка; два противоположных по знаку заряда, равных по абс. величине,- диполь, или M. 1-го порядка; 4 одинаковых по абс. величине заряда, размещённых в вершинах параллелограмма, так что каждая его сторона соединяет заряды противоположного знака,- квадру-поль, или M. 2-го порядка. Название M. включает обозначение числа зарядов (на греч. языке), образующих M ., напр. октуполь (окту - 8) означает, что в состав этого M. входит 8 зарядов. Выделение таких конфигураций связано с описанием полей от сложных, ограниченных в пространстве систем источников. На больших расстояниях (для статич. полей, значительно превышающих размеры системы источников) поле от таких систем устроено относительно просто и может быть описано как суперпозиция полей нек-рого числа M. Это гл. физ. основание для введения понятия M. Осн. характеристика M.- мультипольный момент, к-рый позволяет однозначно связать поля M. с полями сложных систем источников на больших расстояниях. Эта связь приводит к упрощениям широкого класса задач, т. к. поля M. относительно просты в силу повыш. симметрии относительно вращений и перестановок зарядов мультиполь-ных конфигураций.

Введение мультипольного момента основано на довольно простых соображениях, к-рые удобно проиллюстрировать на примере статич. электрич. полей, создаваемых системой точечных зарядов e_i. B системе координат с центром, расположенным где-нибудь внутри системы зарядов, положения зарядов характеризуются радиус-векторами r_i(i - номер заряда). Потенциал этой системы зарядов в точке R. определяется суммой потенциалов всех частиц:

Если интересующая нас точка R значительно удалена от системы зарядов, т. е. |r_i|/|R| << 1, то потенциал можно разложить в Тейлора ряд по степеням этого отношения:

где a_j = 1, 2, 3 - нумеруют компоненты соответствующих векторов; по повторяющимся a_j производится суммирование. Такое разложение потенциала наз. разложением по M. или мультипольным разложением. В нулевом приближении

т. е. f⁽⁰⁾ совпадает с потенциалом точечного заряда q, равного суммарному заряду системы. Величина 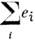- мультипольный момент нулевого порядка - полностью определяет в этом приближении потенциал поля на больших расстояниях. Следующий член разложения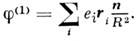

Здесь n - единичный вектор, направленный вдоль R. Величина , определяющая (если q= 0) потенциал в 1-м порядке, наз. динольным моментом системы зарядов или мультипольным моментом 1-го порядка. T. о., характеризуя потенциал (или поле) в 1-м порядке, можно заменить систему зарядов точечным зарядом q и диполем с дипольным моментом d. След. член разложения f⁽²⁾ после нек-рых преобразований записывается в виде

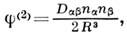
где 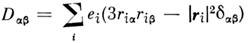(или Q_ab.=D_ab/6) наз. квадрупольным моментом системы зарядов (d_ab - Кро-некера символ).

Общий член разложения потенциала определяется неприводимым тензором l -го ранга

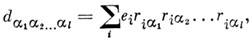
к-рый наз. 2^l -польным моментом системы зарядов, l - порядок M. Тензор 2^l -польного момента симметричен по всем индексам и обращается в нуль при сво-рачивании по любой паре индексов. Общий член разложения потенциала имеет более компактную форму при разложении j(R) по сферическим функциям:

где Y_lm, Y*_lm - сферич. ф-ции, q, f и q_i, j_i - полярный и азимутальный углы, образуемые векторами R и r_i с осями координат. Приведённая форма разложения отличается от исходного ряда Тейлора только перегруппировкой слагаемых и введением сферич. ф-ций, поэтому совокупность 2l + 1 независимых величин Q^(l)_m также наз. 2^l -польным моментом. Если все предыдущие моменты равны нулю, 2^l -польный момент не зависит от выбора начала системы координат.

Полученные соотношения позволяют дать более общее определение M. порядка l как системы зарядов, для к-рой мультипольный момент порядка l отличен от нуля, а все остальные мультипольные моменты равны нулю. Потенциал статич. поля M. порядка l убывает на бесконечности как R^-(l+1). Такой характер спадания математически объясняется тем, что потенциал раскладывается в ряд по обратным степеням R, а физически связан с интерференцией полей от отд. зарядов, входящих в M. Кроме этого, M. обладает специфич. угл. зависимостью, определяемой l -й сферич. ф-цией. Характер убывания поля вдали от сложной системы зарядов позволяет заменить её совокупность M. соответствующего порядка (с соответствующими значениями мультиполь-ных моментов).

Вполне аналогично мультипольное разложение можно ввести для статич. магн. полей, создаваемых системой стационарных токов. Для этого необходимо провести разложение векторного потенциала магн. поля:

u_i - скорость движения i -го заряда. В отличие от случая статич. электрич. полей, разложение потенциала статич. магн. поля начинается с дипольного вклада, т. к. магн. зарядов нет ( магнитные монополи пока не обнаружены). Для первого члена разложения получим

где 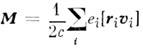- магнитный момент системы.

След. члены разложения получаются аналогично. Общий член разложения векторного потенциала выражается через шаровые ф-ции.

Для непрерывных ограниченных распределений зарядов (источников и стоков) в приведённых выше ф-лах заменяется объёмным интегралом от соответствующей плотности заряда (тока).

Разложение по M. широко используется не только в задачах электро- и магнитостатики, но и в др. областях физики, напр. в акустике и общей теории относительности.

M. применяют также и для исследований полей излучения систем движущихся зарядов (или неременных источников и стоков). Малым параметром, позволяющим описывать поле излучения упрощённым образом, служит отношение размеров области L, в к-рой движутся заряды, к длине излучаемой волны l (L << l). Такое поле излучения можно представить как суперпозицию полей M. с переменными во времени мультипольными моментами. В этом случае возникают три физически различных семейства M.- магн. M., определяемые по-

перечными токами, электрич. M., подразделяющиеся на тороидные [определяемые продольными (радиальными) токами] и зарядовые M., аналогичные обычным эл.-статич. (скалярным) M. (подробнее см. Мульти-польное излучение).

Лит.: Ландау Л. Д., Лифшиц E. M., Теория поля, 7 изд., M., 1988; Ахиезер А. И., Берестецкий В. Б., Квантовая электродинамика, 4 изд., M., 1981.

А. В. Тур, В. В. Яновский.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.