- ЛОКАЛЬНОЕ ТЕРМОДИНАМИЧЕСКОЕ РАВНОВЕСИЕ
- ЛОКАЛЬНОЕ ТЕРМОДИНАМИЧЕСКОЕ РАВНОВЕСИЕ
-
- одно из осн. понятий термодинамики неравновесных процессов и механики сплошных сред;равновесие в очень малых (элементарных) объёмах среды, содержащих всё же столь большое число частиц (молекул, атомов, ионов и др.), что состояние среды в этих физически бесконечно малых объёмах можно характеризовать темп-рой Т(х), хим. потенциалами
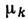( х )и др. термоди-намич. параметрами, но не постоянными, как при полном равновесии, а зависящими от пространств. координат х и времени. Ещё один параметр Л. т. р.- гидро-динамич. скорость и (х) - характеризует скорость движения центра масс элемента среды. При Л. т. р. элементов среды состояние среды в целом неравновесно. Если малые элементы среды рассматривать приближённо как термодинамически равновесные подсистемы и учитывать обмен энергией, импульсом и веществом между ними на основе ур-ний баланса, то задачи термодинамики неравновесных процессов решаются методами термодинамики и механики. В состоянии Л. т. р. плотность энтропии s(z )на единицу массы является ф-цией плотности внутр. энергии 
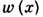и концентраций компонентов с k (x), такой же, как и в состоянии равновесия термодинамического. Термодинамич. равенства остаются справедливыми для элемента среды при движении вдоль пути его центра масс:
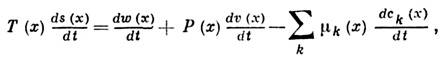
где
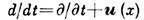grad,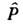 
( х)- давление, 
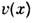- удельный объём.
Статистич. физика позволяет уточнить понятие Л. т. р. и указать пределы его применимости. Понятию Л. т. р. соответствует локально равновесная ф-ция распределения f плотности энергии, импульса и массы, к-рая отвечает максимуму информационной энтропии при заданных ср. значениях этих величин как ф-ций координат и времени:
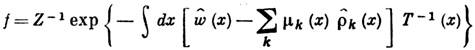
где Z - статистич. сумма,
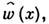
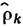( х) - динамич. переменные (ф-ции координат и импульсов всех частиц системы), соответствующие плотности энергии (в системе координат, движущейся с гидродинамич. скоростью) и плотности массы. При помощи такой ф-ции распределения можно определить понятие энтропии неравновесного состояния как энтропии такого локально равновесного состояния, к-рое характеризуется теми же значениями плотностей энергии, импульса и массы, что и рассматриваемое неравновесное состояние. Однако локально равновесное распределение позволяет получать лишь ур-ния т. н. идеальной гидродинамики, в к-рых не учитываются необратимые процессы. Для получения ур-ний гидродинамики, учитывающих необратимые процессы теплопроводности, вязкости и диффузии (т. е. переноса явления), требуется обращаться к кинетич. ур-нию для газов (см. Кинетика физическая )или к Лиувилля уравнению, справедливому для любой среды, и искать такие их решения, к-рые зависят от координат и времени лишь через ср. значения параметров, определяющих неравновесное состояние. В результате получается неравновесная ф-ция распределения, к-рая позволяет вывести все ур-ния, описывающие процессы переноса энергии, импульса и вещества (ур-ния диффузии, теплопроводности и Навье - Стокса уравнения).
Лит.: Гроот С., Мазур П., Неравновесная термодинамика, пер. с англ., М., 1964, гл. 3, p 2; Xаазе Р., Термодинамика необратимых процессов, пер. с нем., М., 1967; 3убарев Д. Н., Неравновесная статистическая термодинамика, М., 1971. 520-22. Д. Н. Зубарев.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
