- ЛИНЕЙНЫЙ ОПЕРАТОР
- ЛИНЕЙНЫЙ ОПЕРАТОР
-
А в векторном пространстве L- отображение, сопоставляющее каждому вектору е век-poro множества D (содержащегося в L и наз. областью определения Л. о.) др. вектор, обозначаемый Ае (и называемый значением Л. о. на векторе е). Выполнены след. условия: 1) D - линейное множество, т. е. для любых его элементов е 1 и е 2 я любых комплексных чисел
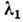 и
и 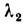 вектор
вектор 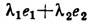 также принадлежит D; 2 )Л. о. переводит линейную комбинацию векторов в ту же линейную комбинацию соответствующих значений:
также принадлежит D; 2 )Л. о. переводит линейную комбинацию векторов в ту же линейную комбинацию соответствующих значений: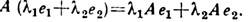
Примеры Л. о.: матрица А =( а ij), действующая в n -мерном евклидовом пространстве по правилу (A е)i=
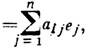 где векторы - столбцы комплексных чисел; дифференциальный оператор A =a0+a1d/dx+...+andn/dxn, определённый равенством (Af) (x) = a0f(x)+а 1df(x)/dx+...+andnf(x)/dxn; интегральный оператор А, определённый соотношением (Af)(x)= dyA
где векторы - столбцы комплексных чисел; дифференциальный оператор A =a0+a1d/dx+...+andn/dxn, определённый равенством (Af) (x) = a0f(x)+а 1df(x)/dx+...+andnf(x)/dxn; интегральный оператор А, определённый соотношением (Af)(x)= dyA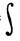 (x, y)f(y).
(x, y)f(y).
Конечномерные пространства. В конечномерном пространстве Л. о. можно определить на всех векторах и задать нек-рой матрицей ( а ij). Если e1 е 2, ..., en- ортонормированный базис, то а ij= ( е i, Ае j), где ( е, f) - скалярное произведение векторов е и f. Если для нек-рого вектоса е и комплексного числа
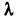 выполнено равенство Ае=
выполнено равенство Ае=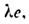 то е наз. собственным вектором (собственной функцией), а
то е наз. собственным вектором (собственной функцией), а 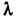 - собственным значением оператора А. Совокупность всех собств. значений наз. дискретным спектром, а множество собств. векторов, отвечающих нек-ро-му собств. значению
- собственным значением оператора А. Совокупность всех собств. значений наз. дискретным спектром, а множество собств. векторов, отвечающих нек-ро-му собств. значению 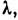 - собств. подпространством Л. о.
- собств. подпространством Л. о.
Конечномерный Л. о. U наз. унитарным, если унитарна его матрица (uij), т. е. если
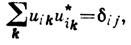
где
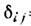 =0 при
=0 при 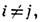 и
и 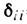 =1. Унитарным является, напр., оператор поворота плоскости на угол
=1. Унитарным является, напр., оператор поворота плоскости на угол 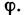 Собств. значения унитарного Л. о. лежат на единичной окружности в комплексной плоскости, т. е.
Собств. значения унитарного Л. о. лежат на единичной окружности в комплексной плоскости, т. е. 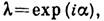 где
где 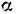 - вещественное число. Унитарные Л. о. оставляют неизменными длины векторов и углы между ними, т. е. сохраняют скалярное произведение: ( е, f) = (Ue, Uf). Унитарные конечномерные Л. о. используют для описания разл. симметрии физ. систем. Совокупность соответствующих Л. о. образует представление группы симметрии.
- вещественное число. Унитарные Л. о. оставляют неизменными длины векторов и углы между ними, т. е. сохраняют скалярное произведение: ( е, f) = (Ue, Uf). Унитарные конечномерные Л. о. используют для описания разл. симметрии физ. систем. Совокупность соответствующих Л. о. образует представление группы симметрии.
Конечномерный оператор
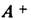 наз. сопряжённым к А, если матрицы этих операторов связаны соотношениями
наз. сопряжённым к А, если матрицы этих операторов связаны соотношениями 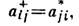 т. е. матрица
т. е. матрица 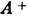 получается из матрицы А в результате транспонирования и комплексного сопряжения. Если
получается из матрицы А в результате транспонирования и комплексного сопряжения. Если 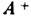 =A то А наз. самосопряжённым или эрмитовым. Пример самосопряжённых конечномерных Л. о.- Паули матрицы, т. е. операторы спина в квантовой механике. Самосопряжённый Л. о. обладает важным свойством вещественности: ( е, Ае)- (е, Ае)
=A то А наз. самосопряжённым или эрмитовым. Пример самосопряжённых конечномерных Л. о.- Паули матрицы, т. е. операторы спина в квантовой механике. Самосопряжённый Л. о. обладает важным свойством вещественности: ( е, Ае)- (е, Ае) . Все собств. значения самосопряжённого оператора также вещественны, а собств. векторы, отвечающие разл. собств. значениям, попарно ортогональны. Ортонормированный базис в конечномерном пространстве можно составить из собств. векторов e1, e2, ..., е n самосопряжённого Л. о. А. В "том базисе матрица Л. о. А диагональна: aij=
. Все собств. значения самосопряжённого оператора также вещественны, а собств. векторы, отвечающие разл. собств. значениям, попарно ортогональны. Ортонормированный базис в конечномерном пространстве можно составить из собств. векторов e1, e2, ..., е n самосопряжённого Л. о. А. В "том базисе матрица Л. о. А диагональна: aij=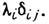
Произведение ( АВ )Л. о. А и В определяется результатом последоват. применения к вектору е операторов В и А, т. е. ( АВ)е=А (Be). Произведение операторов, вообще говоря, не перестановочно:
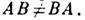 Величина АВ-ВА=[ А , В]наз. коммутатором Л. о. А и В. Если Л.o. коммутируют, т. е. [ А, В] = 0, то Л. о. А и В можно одновременно привести к диагональному виду, т. е. в пространстве существует такой ортонормиров. базис, что каждый его элемент является собственным для А и для В.
Величина АВ-ВА=[ А , В]наз. коммутатором Л. о. А и В. Если Л.o. коммутируют, т. е. [ А, В] = 0, то Л. о. А и В можно одновременно привести к диагональному виду, т. е. в пространстве существует такой ортонормиров. базис, что каждый его элемент является собственным для А и для В.
Самосопряжённый Л. о. Р наз. проекционным оператором или проектором, если Р 2=Р. Для каждого проектора найдётся такое подпространство Lp пространства L, что Ре=е, если е принадлежит Lp, и Ре=0, если е принадлежит ортогональному дополнению Lp. Всякий конечномерный самосопряжённый оператор А можно представить в виде
А =
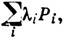 .
.где суммирование проводится по всем собств. значениям
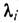 , а Р; - проектор на собств. подпространство, отвечающее
, а Р; - проектор на собств. подпространство, отвечающее 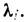 Это равенство наз. спектральным разложением конечномерного самосопряжённого оператора, оно позволяет строить разл. Ф-ции f(A )от самосопряжённого Л. о. A: f(A)- Всякий унитарный Л. о. U в конечномерном
Это равенство наз. спектральным разложением конечномерного самосопряжённого оператора, оно позволяет строить разл. Ф-ции f(A )от самосопряжённого Л. о. A: f(A)- Всякий унитарный Л. о. U в конечномерном 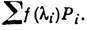 пространстве допускает представление U=ехр(iA), где А - эрмитов Л. о. Если семейство U реализует представление группы симметрии, то соответствующее семейство самосопряжённых Л. о. А задаёт представление Ли алгебры этой группы.
пространстве допускает представление U=ехр(iA), где А - эрмитов Л. о. Если семейство U реализует представление группы симметрии, то соответствующее семейство самосопряжённых Л. о. А задаёт представление Ли алгебры этой группы.
Бесконечномерные пространства. В бесконечномерном гильбертовом пространстве Л. о., вообще говоря, нельзя определить на всех векторах. Обычно область определения D, не исчерпывая всего L, является всюду плотной (т. е. любой вектор из L можно с заданной точностью приблизить вектором из D). На всём пространстве можно задать только т. н. ограниченные (непрерывные) операторы. Л. о. А наз. ограниченным, если существует такая константа С, что для всех векторов е из D выполнено неравенство ( Ае, Ае)
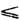 С (е, е). Для неограниченного Л. о. усложняется понятие сопряжённости (подробнее см. Эрмитов оператор). В бесконечномерном случае Л. о. помимо дискретного могут иметь и непрерывный спектр. Число
С (е, е). Для неограниченного Л. о. усложняется понятие сопряжённости (подробнее см. Эрмитов оператор). В бесконечномерном случае Л. о. помимо дискретного могут иметь и непрерывный спектр. Число 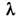 наз. точкой непрерывного спектра, если найдётся такая последовательность е1, е 2, ..., en, ... нормированных векторов, что все они ортогональны каждому собств. вектору оператора А, а при
наз. точкой непрерывного спектра, если найдётся такая последовательность е1, е 2, ..., en, ... нормированных векторов, что все они ортогональны каждому собств. вектору оператора А, а при 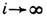 норма векторов
норма векторов 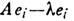 стремится к нулю. Непрерывный и дискретный спектры оператора могут пересекаться. Объединение дискретного и непрерывного спектров паз. просто спектром. Спектр самосопряжённого Л. о. всегда веществен. Видоизменяется спектральное разложение самосопряжённого Л. о.: каждому интервалу вещественной оси от
стремится к нулю. Непрерывный и дискретный спектры оператора могут пересекаться. Объединение дискретного и непрерывного спектров паз. просто спектром. Спектр самосопряжённого Л. о. всегда веществен. Видоизменяется спектральное разложение самосопряжённого Л. о.: каждому интервалу вещественной оси от 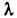 до
до 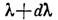 сопоставляется нек-рый проектор
сопоставляется нек-рый проектор 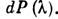 Подпространство, на к-рое проектирует этот проектор, содержит все собств. подпространства оператора А, отвечающие собств. числам
Подпространство, на к-рое проектирует этот проектор, содержит все собств. подпространства оператора А, отвечающие собств. числам 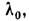 таким, что
таким, что 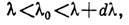 а также подпространство, ответственное за появление непрерывного спектра в интервале от
а также подпространство, ответственное за появление непрерывного спектра в интервале от 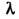 до
до 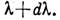
Оказывается, что А= где интеграл является пределом соответствующих
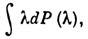 сумм Дарбу, а интегрирование ведётся по всей вещественной оси. Функция f(A) от самосопряжённого Л. о. А определяется интегралом
сумм Дарбу, а интегрирование ведётся по всей вещественной оси. Функция f(A) от самосопряжённого Л. о. А определяется интегралом 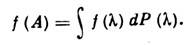
В квантовой теории самосопряжённые Л. о. отвечают наблюдаемым физ. величинам. Процедура квантования сводится к замене евклидовых канонич. координат и импульсов такими самосопряжёнными Л. о., что их коммутаторы совпадают с соответствующими скобками Пуассона. Операторы других наблюдаемых величин выражают при помощи классич. 'ф-л через операторы координат и импульсов.
Лит.: Нейман И., Математические основы квантовой механики, пер. с нем., М., 1964; Дирак П., Принципы квантовой механики, пер. с англ., 2 изд., М., 1979; Кострикин А. И., Манин Ю. И., Линейная алгебра и геометрия, 2 изд., М., 1986; Рихтмайер Р., Принципы современной математической физики, пер. с англ., т. 1, М., 1982.
О. И. Завьялов.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
