ЛЕОНТОВИЧА ПАРАБОЛИЧЕСКОЕ УРАВНЕНИЕ

ЛЕОНТОВИЧА ПАРАБОЛИЧЕСКОЕ УРАВНЕНИЕ

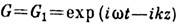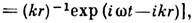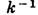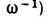- линейное однородное дифференц. ур-ние (аналогичное ур-нию Шрёдингера) для комплексной амплитуды волнового поля. Л. п. у. получается из волнового уравнения, если решение представить в виде и=А (r, t)G(r, t), где G - к.-л. точное решение [напр. для однородной изотропной среды или G== G₂ а А (r, t) - медленная (в масштабе и амплитуда (ф-ция ослабления). Если А - скаляр, a G=G₁, то Л. п. у. имеет вид

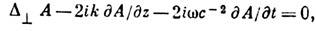
где 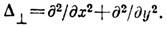В общем случае существует связь характерных масштабов изменения А во времени 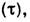вдоль 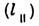и поперёк 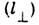направления распространения плоской волны G₁: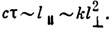

В отличие от геометрической оптики метода, описывающего волновые процессы внутри каждой лучевой трубки независимо, Л. п. у. позволяет учесть эффекты поперечной диффузии А в смежные трубки. При этом, как и в ур-нии Шрёдингера, соответствующий коэф. диффузии является величиной чисто мнимой, поэтому при диффузии изменяются и амплитуда, и фаза поля. Л. п. у. составляет основу матем. аппарата квазиоптики.

Важным классом полей, описываемых Л. п. у., являются гауссовы пучки, структура к-рых имеет автомодельный характер, т. е. с точностью до масштаба сохраняется в любом сечении.

Л. п. у. применяют в разл. задачах асимптотич. теории дифракции: при медленном изменении параметров среды, при расчётах квазиоптич. линий передачи и резонаторов. Возможно также обобщение Л. п. у. на диспергирующие и нелинейные среды, в частности, с его помощью исследованы пространственные структуры в нелинейной оптике, рассчитаны эффекты самофокусировки, параметрич. взаимодействия волн, обращения волнового фронта и т. д.

Лит. см. при ст. Kвазиоптика. С. Н. Власов, М. Л. Левин.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.