КОНВЕКТИВНЫЙ ТЕПЛООБМЕН

КОНВЕКТИВНЫЙ ТЕПЛООБМЕН

- необратимый процесс переноса теплоты в движущихся средах с неоднородным полем темп-ры, обусловленный совместным действием конвекции и молекулярного движения.

Наиб. важный для практики случай - К. т. между движущейся средой и поверхностью её раздела с др. средой (твёрдым телом, жидкостью или газом) - наз. конвективной теплоотдачей. Вследствие вязкости движущейся среды она "прилипает" к поверхности раздела, в результате местная скорость среды относительно этой поверхности равна нулю. Поэтому плотность конвективного теплового потока, подходящего к поверхности раздела (или отходящего от неё), может быть описана с помощью закона теплопроводности (закона Фурье):

где 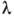- коэф. молекулярной теплопроводности, Т- темп-pa среды. Если 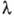характеризует физ. свойства среды, то градиент темп-ры формируется под действием конвективного движения среды. Чем интенсивнее конвекция, тем больше градиент темп-ры. Определение градиента темп-ры у стенки обычно является предметом теоретич. или эксперим. исследования. В зависимости от вида конвективного движения различают К. т. при вынужденной, свободной и капиллярной конвекциях. Могут существовать и смешанные виды К. т.

Теоретич. описание процесса К. т. строится на основе ур-ния сохранения энергии в среде:

где 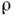- плотность среды, р- давление, с _р - уд. теплоёмкость при пост. давлении,- коэф. динамич. вязкости, Ф - диссипативная функция, учитывающая нагрев среды из-за внутр. трения, Q - внутр. тепловыделение в единице объёма среды, - полная, или субстанциональная, производная по времени т, представляющая собой сумму локальной и конвективной составляющих:

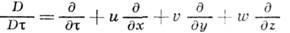
( х, у, z - пространств. координаты, и,, 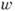- составляющие вектора скорости вдоль осей этих координат).

Для решения ур-ния (2) необходимо знать граничные условия на поверхности раздела и в окружающем пространстве, а также в случае зависимости процесса от времени - нач. условия. Для определения входящих в ур-ние (2) составляющих скорости среды дополнительно привлекаются ур-ния сохранения кол-ва движения в проекции на разл. оси координат.

К. т. может осложняться протеканием в среде или на поверхности раздела разных физ.-хим. превращений (кипение, плавление, конденсация, диссоциация, ионизация и т. п.). В этих случаях для теоретич. описания К. т. используются дополнит. ур-ния, отражающие кинетику отд. физ.-хим. процессов или условия термодинамич. равновесия, напр. законы действующих масс для разл. хим. реакций. Если при этом отд. физ.-хим. превращения протекают на поверхности раздела и имеет место суммарный расход массы через эту поверхность, то вместо ур-ния (1) для описания плотности теплового потока к поверхности раздела используется более общее ур-ние:

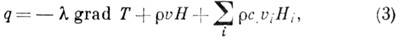
где 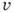- скорость среды в направлении нормали к поверхности, Я - энтальпия среды при темп-ре поверхности, 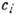- относит. массовые концентрации отд. хим. компонентов, 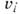- их скорости диффузии в направлении нормали к поверхности, - их энтальпии при темп-ре поверхности раздела, вычисленные с учётом энергии образования этих компонентов при стандартных условиях.

Подходящий к поверхности раздела конвективный тепловой поток удобно представлять в виде закона Ньютона:

где - коэф. конвективного теплообмена, Т - темп-ра поверхности раздела, Т _с - характерная темп-ра среды. В качестве Т _с при обтекании тела безграничным равномерным потоком принимается темп-pa внеш. среды (при больших скоростях среды - темп-pa торможения, или т. н. "равновесная" темп-pa; см. Аэродинамический нагрев), при течении в трубах или процессах К. т. в замкнутых сосудах - среднемассовая темп-ра среды.

Описание процесса К. т. может быть представлено в безразмерном виде с использованием подобия теории. Интенсивность К. т. характеризуется безразмерным критерием - Нусселъта числом, где L - характерный размер. В случае К. т. при вынужденной конвекции осн. определяющим критерием является Рейнолъдса число, где V - скорость среды, - коэф. динамич. вязкости. Кроме числа Рейнольдса влияние на К. т. оказывает Прандтля число= = 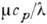и т. н. температурный фактор учитывающий переменность теплофиз. свойств среды при изменении её темп-ры. В результате критериальный закон К. т. при вынужденной конвекции имеет вид

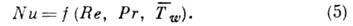
Помимо перечисленных основных определяющих критериев на К. т. при вынужденной конвекции могут оказывать влияние и др. факторы. В частности, при больших скоростях полёта тела в атмосфере важную роль играет Маха число.

Вид зависимости (5) определяется геом. формой поверхности раздела и режимом её обтекания, в частности режимом течения в пограничном слое (ламинарным или турбулентным), наличием и положением зон отрыва потока (см. Отрывное течение). Критериальные законы К. т. в виде (5) могут быть получены как на основании теоретич. расчётов [напр., численным решением системы ур-ний (2) и др.], так и экспериментально - путём исследования теплоотдачи к моделям подобной геом. формы в представляющем интерес диапазоне изменения числа Рейнольдса и др. определяющих критериев. Напр., средний коэф. К. т. в случае поперечного обтекания цилиндра описывается с помощью степенной зависимости Nu= 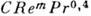, причём С и m имеют разл. значение для разных диапазонов изменения числа Рейнольдса:

	Re	С	m
	5-80	0,923	0,40
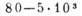
		0,792	0,46
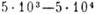
		0, 225	0,60
		0,0262	0,80

При свободной (естественной) конвекции осн. определяющим критерием К. т. является Грасгофа число 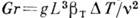, где - ускорение свободного падения, - коэф. объёмного температурного расширения среды, - коэф. кинематич. вязкости, 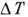- характерный перепад темп-р внутри среды. Критериальный закон принимает вид 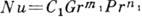. При 0,5 определяющую роль в процессе К. т. играет лея число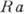,_ объединяющее критерии и :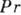

где 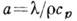- коэф. температуропроводности среды. Напр., средний коэф. К. т. при свободной конвекции бесконечной среды около горизонтального цилиндра н случае описывается степенным законом: 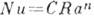, причём С и n связаны с реализуемым режимом течения около цилиндра и могут быть приняты равными значениям, приведённым в табл.

	Ra	С	n
		0,45	0
		1,18	1/8
		0,54	1/4
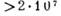
		0, 135	1/3

В случае жидких металлов, для к-рых , определяющую роль в процессе К. т. при свободной конвекции играет комбинированный критерий

При капиллярной конвекции осн. определяющими критериями К. т. являются числа Марангон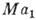и и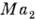

где

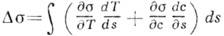
- перепад поверхностного натяжения вследствие изменения темп-ры и концентрации с поверхностно-активного вещества вдоль свободной поверхности.

Лит.: Кутателадзе С. С., Основы теории теплообмена, 5 изд., М., 1979; Теплотехнический справочник, 2 изд., т. 2, М., 1976; Кутателадзе С. С., Б о р и ш а н-с к и и В. М., Справочник по теплопередаче, Л.-М., 1959; Теория теплообмена. Терминология, М., 1971; Основы теплопередачи в авиационной и ракетно-космической технике, М., 1975; Проблемы космического производства, М., 1980.

Н. А. Апфимов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.