КОЛМОГОРОВА - ФЁЛЛЕРА УРАВНЕНИЕ

КОЛМОГОРОВА - ФЁЛЛЕРА УРАВНЕНИЕ

- интегродифференц. ур-ние для переходной плотности вероятности марковских случайных процессов с разрывными (скачкообразными) изменениями состояния. Получено А. Н. Колмогоровым в 1938 и У. Феллером (W. Feller) в 1940.

Пусть, напр., реализации случайного процесса x(t )представляют собой кусочно-постоянные ф-ции, скачком меняющие значения в статистически независимые моменты времени. За малый промежуток времени скачок происходит с вероятностью

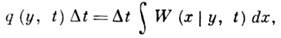
где у - значение процесса в момент t,a 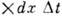- вероятность перескока из у в интервал ( х, x+dx )за время 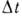. Тогда переходная плотность вероятности для процесса x(t )удовлетворяет К.- Ф. у.:

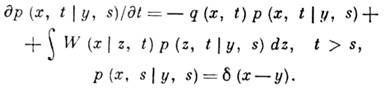
Для марковских процессов с конечным или счётным множеством состояний К.- Ф. у. эквивалентно Колмогорова уравнению. В физ. приложениях встречаются также скачкообразные марковские процессы, непрерывно меняющиеся между моментами скачков. Их переходные плотности вероятности удовлетворяют более общим ур-ниям, в правой части к-рых помимо интегрального члена имеются дифференц. члены, описывающие регулярный снос и диффузию.

Лит.: Ф е л л е р В., Введение в теорию вероятностей и ее приложения, пер. с англ., [3 изд.], т. 1-2, М., 1984; Введение в статистическую радиофизику, ч. 1 - Р ы т о в С. М., Случайные процессы, М., 1976; Тихонов В. И., М и р он о в М. А., Марковские процессы, М., 1977. А. И. Саичев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.