- КВАЗИЧАСТИЦА
- КВАЗИЧАСТИЦА
-
(элементарное возбуждение) - фундаментальное понятие квантовой теории многих тел, введение к-рого радикально упрощает физ. картину и методы описания широкого круга процессов в системах многих частиц с сильным взаимодействием, в т. <ч. в конденсированных средах ( твёрдое тело, квантовая жидкость),плазме, ядре атомном.К.- особый долгоживущий многочастичный комплекс, к-рый, в отличие от обычных (структурных) частиц, составляющих систему, слабо взаимодействует со своим окружением (или, по крайней мере, это взаимодействие сводится к самосогласованному полю). Поэтому К. находится в определ. квантовом состоянии со своей волновой ф-цией, энергией, импульсом (в случае кристалла - квазиимпулъсом), спином и т. д., двигаясь как целое подобно обычной частице (отсюда термин "К."). Будучи коллективным образованием, К. имеет состав, непрерывно обновляющийся при её движении; лишь в предельных случаях этот состав фиксирован как у связанного состояния типа молекулы.
Типы К. По внутр. структуре (при мысленном выключении взаимодействия между частицами) К. делятся на 2 класса. Одночастичное возбуждение представляет собой обычную частицу, обросшую "шубой" за счёт взаимодействия с др. возбуждениями. Такая К. состоит из обычной частицы (или дырки,т. е. свободного состояния в энергетич. распределении яастиц) и её "шубы" - совокупности др. возбуждений системы (пар частица - дырка, фононов и т. д.), к-рые К. вовлекает в своё движение. При выключении взаимодействия К. теряет "шубу", превращаясь в "голую" частицу. Примеры одночастичных возбуждений - электрон проводимости в твёрдом теле (в ионном кристалле он может увлечь за собой созданную им же самим поляризацию решётки, см. Полярон),нуклон в атомном ядре (см. Оболочечная модель ядра), фононно-ротонное возбуждение в жидком 4 Не (см. Сверхтекучесть).При выключении взаимодействия эти К. переходят соответственно в "голые" электрон, нуклон, атом Не. К таким К. можно отнести и распространяющийся по системе заряж. частиц фотон, "шуба" к-рого состоит из испущенных частицами вторичных фотонов. <Коллективное возбуждение (название условно, т. к. любая К.- коллективное образование) представляет собой комплекс, компоненты к-рого равноправны. При выключении взаимодействия эта К. распадается на составные части, к-рые начинают двигаться независимо. К таким К. относятся, напр., Ванье-Momma экситон (связанные состояния электрона проводимости и дырки), плазмон (продольное возбуждение в проводящих средах - см. Плазма, Плазма твёрдых тел).Коллективное возбуждение можно рассматривать как квант, отвечающий (в духе корпускулярно-волнового дуализма) волновому полю, к-рое описывает коллективные колебания соответствующих степеней свободы системы. Так, фонон - квант упругих колебаний, плазмон - квант колебаний плотности заряда, экситон Френкеля - квант колебаний молекул в молекулярном кристалле (см. Молекулярные зкситоны),магнон - квант колебаний спинов в магнитноупорядоченных системах (см. Спиновые волны). Аналогично фононы в кристалле - кванты колебаний кристаллической решётки. При выключении взаимодействия между частицами фонон распадается, превращаясь в совокупность независимых движений частиц, составляющих кристалл. Существуют и более сложные К., представляющие собой комбинации перечисленных выше. Если у двух типов К. в данной системе имеются близкие значения энергии и импульса, то происходит смешивание (гибридизация) таких К. с появлением двух новых К., каждая из к-рых обладает чертами обеих исходных К. Так, смешивание фотона с экситоном или оптич. фононом ведёт к поляритонам (светоэкситонам);смешиванию фотона и магнона отвечает К., наз. светомагнон, смешиванию магнона и поперечного фонона - квант магнитоупругих волн. <Концепция К., формирование к-рой связано с именем Л. Д. Ландау (1941-52), позволила свести сложную динамику системы сильно взаимодействующих частиц к более простой динамике совокупности квазинезависимых объектов. В методе самосогласованного поля такими объектами были сами структурные частицы системы, что позволило описать лишь часть (самосогласованную) взаимодействия между ними. Переход к К. даёт возможность учесть оставшуюся корреляц. часть взаимодействия. Практически проблема сводится к рассмотрению газоподобной системы К., что позволяет описывать мн. равновесные и неравновесные свойства систем с сильным взаимодействием с помощью относительно простых методов статистич. термодинамики и кинетики газов. <Сказанное относится, в частности, к определению тех характеристик системы, к-рые описывают её реакцию (отклик) на внеш. воздействия, ведущие к возбуж дению системы: нагревание (однородное по объёму и отвечающее пост, градиенту темп-ры), приложение разности потенциалов, приведение системы в движение и т. п. Переход системы из основного в близкое по энергии слабо возбуждённое состояние можно свести к рождению внутри системы нек-рого числа квантов возбуждения - К. (отсюда второе назв. К.- "элементарное возбуждение"). Указанные выше характеристики системы определяются динамикой газа таких К. Так, теплоёмкость твёрдого тела сводится к сумме теплоёмкостей газа фононов (см. Решёточная теплоёмкость),газа электронов проводимости и соответствующих "квазидырок" (см. Электронная теплоёмкость )и т. д. Эти же возбуждения определяют коэф. теплои электропроводности твёрдого тела. Вязкость жидкого Не можно найти рассмотрением газа К.- фононов и ротонов. Намагниченность ферромагнетика при Т>0 К слагается из его намагниченности приТ=0К и суммарного магн. момента газа магнонов. <Концепция К. существенно упрощает и решение мн. задач, относящихся к процессу взаимодействия системы мн. частиц с внеш. частицей, позволяя свести этот многочастичный процесс к элементарному акту превращения внеш. частицы в К. (или рождения ею новых К.). Так, поглощение фотона молекулярным кристаллом сводится (при определ. условиях) к превращению фотона в экситон Френкеля; Черенкова- Вавилова излучение быстрой частицы в среде отвечает испусканию частицей фотона, разрешённому законами сохранения энергии и импульса в случае сверхсветовой скорости частицы в среде. Аналогично упрощается описание движения внутри системы влетевшей в неё внеш. частицы и, наоборот, распада системы с вылетом из неё одной из входивших в её состав частиц. Внеш. частица переходит внутри системы в К., и её движение описывается ур-нием Шрёдингера для К. в эффективном внеш. поле (оптич. потенциал в теории ядерных реакций, см. Оптическая модель ядра),распадная же частица возникает из соответствующей К., свойства к-рой определяют характеристики распада (его спектр, время жизни и т. п.).Характеристики К. Для практич. применения концепции К. необходима информация о пределах её применимости, о величинах, характеризующих К., и т. п. В микроскопич. подходе эту информацию дают хорошо разработанные квантово-полевые методы теории мн. тел (см. Грина функция). В феноменологич. теориях, для к-рых концепция К. служит исходным пунктом, напр., в теории сверхтекучести, ферми-жидкости (применительно к электронам металла и нуклонам ядерного вещества), эта информация заимствуется из опыта. <Первичной характеристикой К. служит её спин. К. с целым спином (фотон, фонон, ротон, экситон, плазмон, магнон, пара Купера, поляритон и др.) подчиняются Базе - Эйнштейна статистике; при возбуждении системы они могут рождаться поодиночке. К. с полуцелым спином (электрон, нуклон, полярон и др.) удовлетворяют Ферми - Дирака статистике и должны рождаться и исчезать парами, чтобы изменение полного момента количества движения системы было кратно величине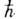 . Это относится к возбуждению системы при неизменном числе её частиц, т. е. в отсутствие "лишней" или распадной частицы (см. выше). В простейшем случае однородной изотропной системы и Т=0К эта пара состоит из К. с импульсом р>р 0 и квазидырки с импульсом p<p0,где р0 - радиус заполненной К. сферы Ферми, связанный с плотностью числа частиц системы (n) тем же соотношением
. Это относится к возбуждению системы при неизменном числе её частиц, т. е. в отсутствие "лишней" или распадной частицы (см. выше). В простейшем случае однородной изотропной системы и Т=0К эта пара состоит из К. с импульсом р>р 0 и квазидырки с импульсом p<p0,где р0 - радиус заполненной К. сферы Ферми, связанный с плотностью числа частиц системы (n) тем же соотношением 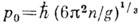 , g - фактор вырождения уровня, как и в идеальном газе (Латтинджера - Уорда теорема). Возбуждение системы сводится тем самым к переходу К. из заполненной области импульсного пространства в незаполненную. Качественно эта картина сохраняет свою силу и в случае кристалла, хотя при этом меняется геометрия ферми-поверхности, отделяющей заполненную К. область от незаполненной, и даже её топология. <Др. важной характеристикой К. является закон дисперсии - зависимость её энергии Eот импульса (или квазиимпульса) р, а также спектр возбуждений системы, т. е. мин. энергия, отвечающая возбуждению системы с данным импульсом и с рождением К. данного типа. Для возбуждений бозевского типа понятие "спектр возбуждения" и дисперсии закон К. совпадают; для возбуждений фермиевского типа спектр возбуждения равен сумме законов дисперсии К. (положительного) и квазидырки (отрицательного). Закон дисперсии К. определяется гл. обр. характером взаимодействия между структурными частицами системы (если существенно самосогласованное взаимодействие между К., то может появиться и зависимость от плотности К., т. е. от темп-ры системы). В микроскопич, подходе закон дисперсии определяется полюсом соответствующей ф-ции Грина (G) в импульсно-энергетич. представлении G(E, р )в нижней полуплоскости энергии E:
, g - фактор вырождения уровня, как и в идеальном газе (Латтинджера - Уорда теорема). Возбуждение системы сводится тем самым к переходу К. из заполненной области импульсного пространства в незаполненную. Качественно эта картина сохраняет свою силу и в случае кристалла, хотя при этом меняется геометрия ферми-поверхности, отделяющей заполненную К. область от незаполненной, и даже её топология. <Др. важной характеристикой К. является закон дисперсии - зависимость её энергии Eот импульса (или квазиимпульса) р, а также спектр возбуждений системы, т. е. мин. энергия, отвечающая возбуждению системы с данным импульсом и с рождением К. данного типа. Для возбуждений бозевского типа понятие "спектр возбуждения" и дисперсии закон К. совпадают; для возбуждений фермиевского типа спектр возбуждения равен сумме законов дисперсии К. (положительного) и квазидырки (отрицательного). Закон дисперсии К. определяется гл. обр. характером взаимодействия между структурными частицами системы (если существенно самосогласованное взаимодействие между К., то может появиться и зависимость от плотности К., т. е. от темп-ры системы). В микроскопич, подходе закон дисперсии определяется полюсом соответствующей ф-ции Грина (G) в импульсно-энергетич. представлении G(E, р )в нижней полуплоскости энергии E:G-1[E(p), р]=0. (1)
Для К. фермионного типа, напр. электрона и нуклона, имеется в виду одночастичная фермионная ф-ция Грина; для К. типа экситона Ванье - Мотта или плазмона - парная ф-ция Грина типа "частица - дырка". Как правило, закон дисперсии, определяемый (1), является комплексной ф-цией:
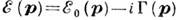 с отрицат. мнимой частью. Волновая ф-ция К. пропорциональна
с отрицат. мнимой частью. Волновая ф-ция К. пропорциональна 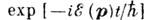 , гдеt - время, и содержит фактор
, гдеt - время, и содержит фактор 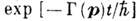 , к-рый описывает "распад" К., т. е. всевозможные процессы, ведущие к её "уходу" из начального состояния. Поэтому величина Г имеет смысл "затухания" К., а обратная величина
, к-рый описывает "распад" К., т. е. всевозможные процессы, ведущие к её "уходу" из начального состояния. Поэтому величина Г имеет смысл "затухания" К., а обратная величина 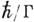 - её времени жизни. Величина
- её времени жизни. Величина 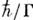 играет важную роль для формулировки критерия применимости концепции квазичастицы: К. действительно представляет собой многочастичный комплекс, движущийся квазинезависимо, если его время жизни велико, т. е. "затухание" Г мало:
играет важную роль для формулировки критерия применимости концепции квазичастицы: К. действительно представляет собой многочастичный комплекс, движущийся квазинезависимо, если его время жизни велико, т. е. "затухание" Г мало:
Для выполнения (2) необходимо, чтобы система находилась в слабо возбуждённом состоянии, т. е. чтобы импульсы бозевских возбуждений были малы (длинноволновой случай), а импульсы фермиевских возбуждений были близки к величине р0;при этом распад (превращение её в др. К.), если и разрешён, то отвечает малому фазовому объёму, а рассеяние К. друг на друге играет малую роль в силу малости их концентрации. Для термически возбуждённой системы сказанное отвечает случаю относительно низких темп-р. Хотя К. и является коллективным образованием и имеет сложную структуру, наличие жёсткой связи еёэнергии с импульсом движения как целого роднит К. (при ГЪE0) с обычной частицей, позволяя, в частности, ввести скорость К.: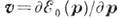 , эффективную массу
, эффективную массу 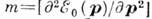 и др. Мн. К. имеют непрерывный спектр возбуждения, для к-рого E0(p)=0 при нек-ром р (обычно при р=0); среди них выделяются К. с акустич. спектром E0=vp при малых р. К ним относятся, в частности, К., отвечающие колебаниям тех степеней свободы, по к-рым в системе произошло спонтанное нарушение симметрии (см. Голдстоуна теорема).Эти К. не имеют порога рождения и появляются в системе при сколь угодно малой энергии возбуждения. Непрерывный спектр имеют акустич. фононы (их спектр определяется показателем преломления среды), нек-рые типы магнонов и др., а также пары К.- квазидырка в несверхпроводящем веществе, энергия к-рых стремится к 0 при приближении импульсов их компонент к поверхности Ферми. <У остальных К. по разным причинам в спектре возбуждения появляется энергетич. щель, равная минимальному (отличному от 0) значению ф-ции E0( р). Для рождения таких К. нужно преодолеть энергетич. порог, равный ширине щели (отсюда, напр., следует, что их вклад в теплоёмкость системы в области низких темп-р экспоненциально мал). К ним относятся плазмоны, у к-рых возникновение щели связано с дальнодействием кулоновских сил, оптич. фононы, экситоны, ротоны, магноны и т. д. Энергетич. щель, равную ширине запрещённой зоны Eg,имеют и электроны в диэлектриках и полупроводниках (см. Зонная теория).Важнейшим примером возбуждения с энергетич. щелью могут служить К. в сверхпроводниках, где для разрыва пары Купера и появления К. в свободном состоянии необходимо затратить конечную энергию. Важную роль играют также характеристики, к-рые описывают взаимодействие К. с др. К., с примесями и дефектами решётки и т. п. (амплитуды и сечения рассеяния), а также характеристики, к-рые определяют длину свободного пробега К., входящую в выражения для кинетич. коэф. системы.
и др. Мн. К. имеют непрерывный спектр возбуждения, для к-рого E0(p)=0 при нек-ром р (обычно при р=0); среди них выделяются К. с акустич. спектром E0=vp при малых р. К ним относятся, в частности, К., отвечающие колебаниям тех степеней свободы, по к-рым в системе произошло спонтанное нарушение симметрии (см. Голдстоуна теорема).Эти К. не имеют порога рождения и появляются в системе при сколь угодно малой энергии возбуждения. Непрерывный спектр имеют акустич. фононы (их спектр определяется показателем преломления среды), нек-рые типы магнонов и др., а также пары К.- квазидырка в несверхпроводящем веществе, энергия к-рых стремится к 0 при приближении импульсов их компонент к поверхности Ферми. <У остальных К. по разным причинам в спектре возбуждения появляется энергетич. щель, равная минимальному (отличному от 0) значению ф-ции E0( р). Для рождения таких К. нужно преодолеть энергетич. порог, равный ширине щели (отсюда, напр., следует, что их вклад в теплоёмкость системы в области низких темп-р экспоненциально мал). К ним относятся плазмоны, у к-рых возникновение щели связано с дальнодействием кулоновских сил, оптич. фононы, экситоны, ротоны, магноны и т. д. Энергетич. щель, равную ширине запрещённой зоны Eg,имеют и электроны в диэлектриках и полупроводниках (см. Зонная теория).Важнейшим примером возбуждения с энергетич. щелью могут служить К. в сверхпроводниках, где для разрыва пары Купера и появления К. в свободном состоянии необходимо затратить конечную энергию. Важную роль играют также характеристики, к-рые описывают взаимодействие К. с др. К., с примесями и дефектами решётки и т. п. (амплитуды и сечения рассеяния), а также характеристики, к-рые определяют длину свободного пробега К., входящую в выражения для кинетич. коэф. системы.
Термодинамика газа К. Зная характеристики К., можно получить термодинамич. описание системы мн. частиц с сильным взаимодействием при Т№0 К, исходя (в первом приближении) из картины идеального газа К. В основе такого описания лежит ф-ция распределения К. по импульсам n(р),к-рая входит в выражения для полной энергии системы: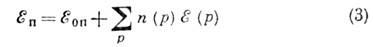
(E0п- энергия при Т=0 К) и её энтропии: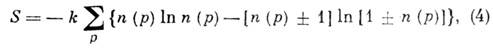
отвечающие модели идеального газа К. (знаки + и - соответствуют К. фермиевского и бозевского типа). Минимум свободной энергии F=U-TSпо n(р)ведёт к выражениям для равновесной ф-ции распределения: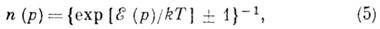
к-рые совпадают с обычными распределениями Ферми и Бозе с равным нулю химическим потенциалом (число К. не фиксировано, а само определяется условиями равновесия). Выражения (3) - (5) и содержат полную термодинамич. информацию о системе (в частности, теплоёмкость системы определяется общим выражением CV=TdS/dT).
К. и квантовая теория поля. В нерелятивистской теории систем мн. частиц последние рассматриваются как бесструктурные объекты с заданными свойствами, что и лежит в основе их отличия от коллективных образований - К. Однако с точки зрения квантовой теории поля и обычные частицы (электроны, фотоны и т. п.) непрерывно взаимодействуют с физ. вакуумом, приобретают за счёт этого внутр. структуру и поэтому ничем в принципе не отличаются от К. Лит.: Абрикосов А. А., Горьков Л. П., Дэялошинский И. Е., Методы квантовой теории поля в статистической физике, М., 1962; Киржаиц Д. А., Полевые методы теории многих частиц, М., 1963; Мигдал А. Б., Теория конечных ферми-систем и свойства атомных ядер, 2 изд., М., 1983; Пайнс Д., Элементарные возбуждения в твёрдых телах, пер. с англ., М., 1965; Каганов М. И., Лифшиц И. М., Квазичастицы, М., 1976. Д. А. Киржниц.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
