КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ

- преобразования q, p "Q(p, q), Р( р, q )(обобщённых) координат и (обобщённых) импульсов, сохраняющие Пуассона скобки:

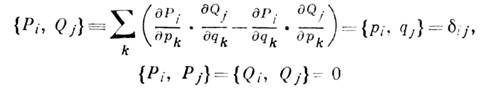
(k=l, . . ., п, п - число степеней свободы системы, d_ij- Кронекера символ). К. п. сохраняют канонич. вид Гамильтона уравнений и нормировку Гамильтона функции Н (р, q, t). При К. п. фигурирующее в вариационном наименьшего действия принципе выражение может меняться лишь на полный дифференциал:

Здесь F - производящая функция К. п, Если она зависит от старых и новых координат, F(q,Q), то явный вид К. п. находится из соотношений р _i=Р Fl Р q,P_i= Р F/ РQ_i, а новая ф-ция Гамильтона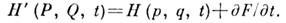

Остальные возможности (всего их 2²ⁿ, когда F зависит от i старых координат, n -iстарых импульсов, j новых координат и n - j новых импульсов, получаются из данной Лежандра преобразованием. К. п. сохраняют интеграл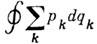 по замкнутойкривой в фазовом пространстве и элемент фазового объёма . Последнее обстоятельство используется при заменах переменных в функциональном интеграле. Для F, не зависящих явно от времени, сохраняется и ф-ция Гамильтона. Для тождественного К. п. . Бесконечно малые К. п. с F= удовлетворяют ур-ниям Гамильтона 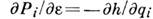, 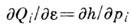с ф-цией Гамильтона h=f(P, q; 0). Поэтому движение системы (параметр e интерпретируется как время t )само есть К. п. Преобразования симметрии, сохраняющие действие 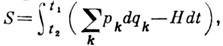очевидным образом являются К. п. <Благодаря свойствам К. п. равноправны все выборы канонич. переменных классич. системы: в её фазовомпространстве можно взять любую систему координат, связанную К. п. с декартовой, в к-рой q, p - обычные координаты и импульсы. <В квантовой механике такого равноправия нет. Постулат канонического квантования, заменяющий скобки Пуассона { р_i, q_j}=d_ij канонич. перестановочными соотношениями 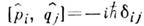, формулируется для декартовой системы координат. Конкретный выбор гильбертова пространства H векторов состояний системы и реализация 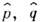как самосопряжённых (эрмитовых) операторов в этом пространстве (их общая область определения должна быть плотной в H)наз. представлением. К. п. в квантовой механике наз. преобразования представлений, сохраняющие канонич. перестановочные соотношения (см. Представлений теория). Для систем с конечным числом степеней свободы все представления канонич. перестановочных соотношений унитарно эквивалентны (теорема фон Неймана): для любых двух представлений операторов и векторов состояний y,y' существует унитарный оператор U, такой, что 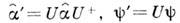(знак + означает эрмитово сопряжение). Т. о., К. п. конечномерных квантовых систем всегда могут быть реализованы как унитарные преобразования, и поэтому они сохраняют спектры операторов, средние значения и др. динамич. характеристики. Напр., переход от шрёдингерова к гейзенбергову описанию эволюции системы (см. Шрёдингера представление, Гейзенберга представление )является унитарным преобразованием, зависящим от времени, с 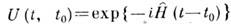, где 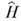- оператор Гамильтона (гамильтониан). Для бесконечномерных квантовых систем теорема фон Неймана неверна: существуют К. п., не сводящиеся к унитарным, и соответственно неэквивалентные представления канонич. перестановочных соотношений. Такие К. п. могут менять спектры операторов и в этом случае дают матем. описание важных физ. эффектов - появление голдстоуновских бозонов при спонтанном нарушении симметрии, Хиггса механизм, изменение спектра состояний системы при фазовых переходах и др. К. п. является стандартным приёмом нахождения спектра элементарных возбуждений ( квазичастиц )в статистич. физике. Примером такого К. п. служат Боголюбова канонические преобразования, с помощью к-рых находятся эти спектры для слабонеидеальных бозе- и ферми-систем. Лит.: Голдстейн Г., Классическая механика, пер. с англ., 2 изд., М., 1975: Диран П., Принципы квантовой механики, пер. с англ., 2 изд., М., 1979; Березин Ф. А. Метод вторичного квантования, 2 изд., М.. 1986; Арнльд В. И., Математические методы классической механики, 2 изд., М., 1979; Эмх Ж., Алгебраические методы в статистической механике и квантовой теории поля, пер. с англ., М., 1976. Б. В. Медведев, В. П. Павлов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.