- ВИНЕРОВСКЙЙ СЛУЧАЙНЫЙ ПРОЦЕСС
- ВИНЕРОВСКЙЙ СЛУЧАЙНЫЙ ПРОЦЕСС
-
- нормальный марковский случайный процесс x(t )с независимыми приращениями. В любой момент времени t распределение вероятностей В. с. п.-гауссово (нормальное). Плотность вероятности В. с. п. в одномерном случае равна
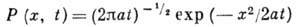и удовлетворяет диффузии уравнению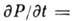
, где а- коэф. диффузии. Плотность распределения приращений 
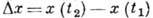за время 
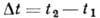равна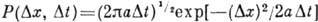 
Распределение вероятностей В. с. п. изучено H. Винером в 1923. Cp. значение В. с. п. равно нулю,
=0, а дисперсия линейно растёт со временем: 
, корреляц. ф-ция В. с. п. определяется выражением
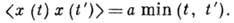
Траектории B. с. п. непрерывны, но нигде не дифференцируемы. Производная В. с. п. -обобщённый случайный процесс п (t) - наз. белым шумом (стационарный нормальный случайный процесс с независимыми значениями, нулевым ср. значением и дельтаобразной корреляц. ф-цией,
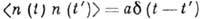). В. с. п. - общепринятая модель броуновского движения, описывает флуктуации фазы в автогенераторах и лазерах. Лит.: Кац M., Вероятность и смежные вопросы в физике, пер. с англ., M., 1965; Ахманов С. А., Дьяков Ю. E., Чиркин А. С., Введение в статистическую радиофизику и оптику, M., 1981. P. А. Минлос.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
