БОЗЕ-ЭЙНШТЕЙНА КОНДЕНСАЦИЯ

БОЗЕ-ЭЙНШТЕЙНА КОНДЕНСАЦИЯ

(бозе-конденсация) - квантовое явление, состоящее в том, что в системе из большого числа частиц, подчиняющихся Бозе - Эйнштейна статистике (бозе-газ или бозе-жидкость), при темп-pax ниже вырождения температуры в состоянии с нулевым имяульсом оказывается конечная доля всех частиц системы. Термин "Б.-Э. к." основан на аналогии этого явления с конденсацией газа в жидкость, хотя эти явления совершенно различны, т. к. при Б.- Э. к. она происходит в пространстве импульсов, а распределение частиц в координатном пространстве не меняется. Теория Б.- Э. к. построена А. Эйнштейном (A. Einstein) в 1925 и развита Ф. Лондоном (F. London) в 1938.

Поскольку Б.- Э. к. происходит даже в идеальном бозе-газе, её причиной являются свойства симметрии волновой ф-ции частиц, а не взаимодействия между ними. Для идеального бозе-газа из Бозе - Эйнштейна распределения

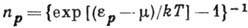
(где T - абс. темп-pa, e _р - энергия частицы с импульсом 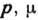- хим. потенциал) следует, что в низшем энергетич. состоянии с 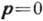находится 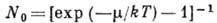частиц. Из положительности 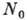следует, что 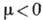Если фактор вырождения 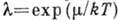близок к 1, то в состоянии с 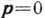может быть очень много частиц. Поэтому нельзя пренебрегать вкладом частиц с 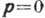при вычислении ср. величин. Из условия постоянства полного числа частиц 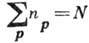в объёме V следует ур-ние для :

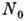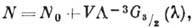
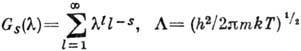- длина волны де-Бройля, соответствующая тепловому движению, т - масса частицы. Отсюда 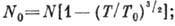T₀- темп-pa бозе-конденсации, или темп-pa вырождения, находится из условия 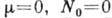, к-рое записывают в след. виде: .

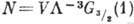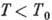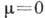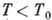При T=0 все частицы находятся в конденсате, при в конденсате находится лишь N₀ частиц, а остальные подчиняются распределению Бозе - Эйнштейна с . При давление оказывается ф-цией только темп-ры 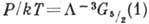и не зависит от объёма, т. к. частицы конденсата, не обладая импульсом, не дают вклада в давление. При 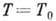производная теплоёмкости испытывает конечный скачок, а сама теплоёмкость, энергия и давление остаются непрерывными, следовательно система совершает своеобразный фазовый переход.

Для жидкого ⁴He в модели идеального газа темп-ра вырождения 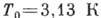близка темп-ре перехода в сверхтекучее состояние, равной 2,18 К, но это не означает, что переход в сверхтекучее состояние есть Б.- Э. к. идеального газа, т. к. для явления сверхтекучести существенно взаимодействие между атомами. В неидеальном бозе-газе явление Б.- Э. к. сохраняется, а неидеальность приводит к появлению частиц с ненулевым импульсом даже при 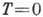, в слабонеидеальном бозе-газе малой плотности

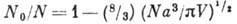
при 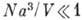, где а - длина рассеяния для потенциала взаимодействия. Если плотность не мала, то число частиц в конденсате можно оценить вариационным методом. Для бозе-жидкости со взаимодействием молекул как твёрдых сфер диаметра b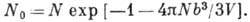

Для 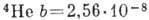см, 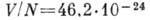см ³, поэтому 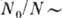0,08. По оценкам, основанным на рассеянии нейтронов, плотность конденсата в 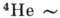неск. % и обладает примерно такой же температурной зависимостью, как и плотность сверхтекучей компоненты. Однако плотность частиц конденсата и плотность сверхтекучей компоненты нельзя отождествить, т. к. при T=0 К вся жидкость является сверхтекучей, хотя не все её частицы находятся в конденсате.

Б.- Э. к. приводит к квантовой когерентности волн де Бройля на макроскопич. масштабах. Конденсат описывается волновой ф-цией, когерентной во всем объёме. При Б.- Э. к. происходит спонтанное нарушение симметрии, связанной с инвариантностью гамильтониана системы относительно калибровочных преобразований; состояние с конечной плотностью конденсата не является калибровочно инвариантным.

Сверхпроводимость можно рассматривать как следствие Б.-Э. к. коррелированных куперовских пар электронов с противоположно направленными импульсами и спинами.

Лит.: Эйнштейн А., Собр. научных трудов, т. 3, M., 1966; Lоndоn F., On the Bose-Einstein condensation, "Phys. Rev.", 1938, v. 54, p. 947. См. также лит. при ст. Статистическая физика. Д. H. Зубарев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.