- СТРУНА
- СТРУНА
-
в теории колебаний, тонкая, гибкая, сильно натянутая нить с равномерно распределённой по длине плотностью. При возбуждении С., напр. ударом или щипком, она начинает совершать колебат. движения, при к-рых все её участки смещаются в поперечном направлении. Любое колебание С. можно представить в виде суммы её гармонич. собств. колебаний, частоты к-рых f зависят от её длины l, площади сечения S, натяжения Q, плотности материала r, а также от условий закрепления концов. Для С., закреплённой на жёстких опорах, fn=(n/2l)?(Q/rS), где n -целое число, соответствующее номеру гармонич. составляющей. Заданное в нач. момент распределение смещений, т. е. способ возбуждения С., определяет спектр возбуждённых собств. колебаний. С.— простейшая колебат. система с распределёнными параметрами.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- СТРУНА
-
в а к у с т и к е - тонкая, гибкая, сильно натянутая нить с равномерно распределённой по длине плотностью. Под это определение подходят как С. музыкальных инструментов, так и шнур, трос или резиновый жгут. С.- простейшая колебат. система с распределёнными параметрами. Малые поперечные смещения у точек С. от положения равновесия описываются волновым ур-нием
где F- сила натяжения, t - время, х - координата вдоль С., r-линейная плотность струны. Согласно ур-нию (*), ускорение нек-рого элемента С. прямо пропорционально кривизне С. в области этого элемента. Решение ур-ния (*) может быть представлено в виде бегущих волн, расходящихся из точки возбуждения в разные стороны:
где
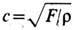-скорость распространения возмущения. В точках закрепления С. происходят отражения волн, причём условия отражения зависят от податливости опор. В случае абсолютно жёстких опор имеет место полное отражение и картина распределения смещений у повторяется через промежутки времени 2l/ с, где l -длина С., т. е. устанавливаются колебания с периодом Т = с/2l. Наличие опор (граничные условия) определяет частоты возможных колебаний С. wn, к-рые кратны наинизшей (основной) частоте
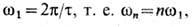
n= 1, 2, 3... Конкретная картина колебаний С. определяется не только граничными условиями, но и способом возбуждения С.
При возбуждении в С. стоячих волн точки С. имеют разные амплитуды смещений, но движутся синхронно, прогибы всех точек одновременно достигают своих макс. и мин. значений. Произвольное возмущение закреплённой С. может быть представлено в виде суммы ее собств. гармонич. колебаний с частотами wn и амплитудами смещений А n. Наибольшая энергия колебаний приходится на осн. частоту w1 а с увеличением номера п энергия собств. колебаний падает и становится тем меньше, чем больше номер частоты. Соответственно струна излучает звук, характеризуемый осн. тоном и обертонами. Последние создают тональную окраску звука - тембр. Полная энергия колебания струны W определяется энергиями отд. собств. колебаний и равна
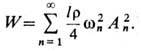
Её можно представить как сумму энергий осцилляторов с массами, равными половине массы струны и совершающими колебания с частотами wn и амплитудами А n.
При колебаниях С. в воздухе отдаваемая ею звуковая энергия невелика. Большая поверхность подставки, на к-рой закрепляется С., напр. дека музыкальных инструментов, обусловливает более эфф. излучение звуковой энергии. Специфику звучания струнному музыкальному инструменту придаёт способ возбуждения С. Так, при возбуждении С. ударом осн. тон насыщен обертонами, а при возбуждении С. щипком роль обертонов относительно невелика.
Лит.: Морз Ф., Колебания и звук, пер. с англ., М.- Л., 1949; Горелик Г. С., Колебания и волны, 2 изд., М., 1959; Скучик Е., Простые и сложные колебательные системы, пер. с англ., М., 1971.
С. В. Егерев.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
