ШРЕДИНГЕРА УРАВНЕНИЕ

ШРЕДИНГЕРА УРАВНЕНИЕ

       

основное динамич. ур-ние нерелятив. квант. механики; предложено австр. физиком Э. Шрёдингером (Е. Schr?dinger) в 1926. В квант. механике Ш. <у. играет такую же фундам. роль, как ур-ния движения Ньютона в классич. механике и Максвелла уравнения в классич. теории электромагнетизма. Ш. у. описывает изменение во времени состояния квант. объектов, характеризуемого волновой функцией. Если известна волн. ф-ция y в нач. момент времени, то, решая Ш. у., можно найти y в любой последующий момент времени t.

Для ч-цы массы т, движущейся под действием силы, порождаемой потенциалом V(x, у, z, t), Ш. у. имеет вид: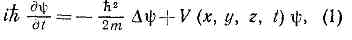

где D=д2/дx2+д2/дy2+д2/дz2 — т. н. оператор Лапласа (х, у, z — координаты). Это ур-ние наз. в р е м е н н ы м Ш. у.

Если V не зависит от времени, то решения Ш. у. можно представить в виде:

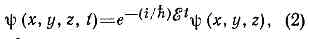где ? — полная энергия квант. системы, a y(x, у, z) удовлетворяет с т а ц и о н а р н о м у Ш. у:

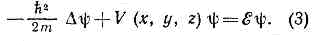Для квант. систем, движение к-рых происходит в огранич. области пр-ва, решения Ш. у. существуют только для нек-рых дискр. значений энергии: ?1, ?2,. . ., ?n, . . .; члены этого ряда (в общем случае бесконечного) нумеруются набором целых квант. чисел п. Каждому значению ?n соответствует волн. ф-ция yn(x, у, z), и знание полного набора этих ф-ций позволяет вычислить все измеримые хар-ки квант. системы.

Ш. у. явл. матем. выражением фундам. св-ва микрочастиц — корпускулярного-волнового дуализма, согласно к-рому все существующие в. природе ч-цы материи наделены также волн. св-вами. Ш. у. удовлетворяет соответствия принципу и в предельном случае, когда длины волн де Бройля значительно меньше размеров, характерных для рассматриваемого движения, позволяет описать движение ч-ц по законам классич. механики. Переход от Ш. у. к ур-ниям классич. механики, описывающей движения ч-ц по траекториям, подобен переходу от волн. оптики к геометрической. Аналогия между классич. механикой и геом. оптикой, к-рая явл. предельным случаем волновой, сыграла важную роль в установлении Ш. у.

С матем. точки зрения Ш. у. есть волн. ур-ние и по своей структуре подобно ур-нию, описывающему колебания нагруж. струны. Однако, в отличие от решений ур-ния колебаний струны, к-рые дают геом. форму струны в данный момент времени, решения y(x, у, z, t) Ш. у. прямого физ. смысла не имеют. Смысл имеет квадрат волн. ф-ции, а именно величина rn(х, у, z, t) =?yn(x, у, z, t)?2, равная вероятности нахождения ч-цы (системы) в момент t в квант. состоянии n в точке пр-ва с координатами х, у, z. Эта вероятностная интерпретация волн. ф-ции — один из осн. постулатов квант. механики.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ШРЁДИНГЕРА УРАВНЕНИЕ

- основное динамич. ур-ние нерелятивистской квантовой механики; предложено Э. Шрёдингером (E. Schrodinger) в 1926. В квантовой механике Ш. у. играет такую же фундам. роль, как ур-ния движения Ньютона в классич. механике и Максвелла уравнения в классич. теории электромагнетизма. Ш. у. описывает изменение во времени состояния квантовых объектов, характеризуемого волновой функцией. Если известна волновая ф-ция 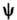в нач. момент времени, то, решая Ш. у., можно найти 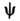в любой последующий момент времени t.

Для частицы массой т, движущейся под действием силы, порождаемой потенциалом 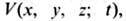Ш. у.

имеет вид

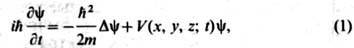
где 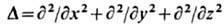-оператор Лапласа, х, у,

z- координаты. Это ур-ние наз. временным Ш. у.

Если V не зависит от времени, то решения Ш. у. можно представить 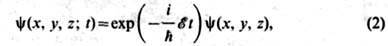в виде

где 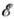-полная энергия квантовой системы, а 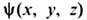удовлетворяет стационарному Ш. у.: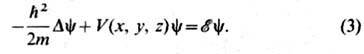

Для квантовых систем, движение к-рых происходит в огранич. области пространства, решения Ш. у. существуют только для нек-рых дискретных значений энергии: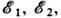... ,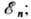члены этого ряда (в общем случае бесконечного) нумеруются набором целых квантовых чисел п. Каждому значению 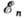соответствует волновая ф-ция 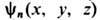и знание полного набора этих ф-ций позволяет вычислить все измеримые характеристики квантовой системы.

Ш. у. является матем. выражением фундам. свойства микрочастиц - корпускулярно-волнового дуализма, согласно к-рому все существующие в природе частицы материи наделены также волновыми свойствами. Ш. у. удовлетворяет соответствия принципу и в предельном случае, когда длины волн де Бройля значительно меньше размеров, характерных для рассматриваемого движения, позволяет описать движение частиц по законам классич. механики. Переход от Ш. у. к ур-ниям классич. механики, описывающей движения частиц по траекториям, подобен переходу от волновой оптики к геометрической. Аналогия между классич. механикой и геом. оптикой, к-рая является предельным случаем волновой, сыграла важную роль в установлении Ш. у.

С матем. точки зрения Ш. у. есть волновое ур-ние и по своей структуре подобно ур-нию, описывающему колебания нагруженной струны. Однако, в отличие от решений ур-ния колебаний струны, к-рые дают геом. форму струны в данный момент времени, решения 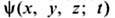Ш. у. прямого физ. смысла не имеют. Смысл имеет квадрат модуля волновой ф-ции, а именно величина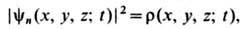

равная вероятности нахождения частицы (системы) в момент t в квантовом состоянии n в точке пространства с координатами 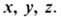Эта вероятностная интерпретация волновой ф-ции - один из осн. постулатов квантовой механики.

Лит.: Шредингер Э., Новые пути в физике. Статьи и речи, пер. с нем., M., 1971; см. также лит. при ст. Квантовая механика.

Л. И. Пономарёв.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.