АВТОМОДЕЛЬНОЕ ТЕЧЕНИЕ

АВТОМОДЕЛЬНОЕ ТЕЧЕНИЕ

       

(от греч. autos — сам и франц. modele — образец), течение жидкости (газа), к-рое остаётся механически подобным самому себе при изменении одного или неск. параметров, определяющих это течение. В механически подобных явлениях наряду с пропорциональностью геом. размеров соблюдается пропорциональность механич. величин — скоростей, давлений, сил и др. (см. ПОДОБИЯ ТЕОРИЯ). Условием автомодельности явл. отсутствие в рассматриваемой стационарной или нестационарной задаче характерных линейных размеров. Стационарное А. т. образуется, напр., при обтекании кругового бесконечного конуса сверхзвук. потоком идеального газа, Картина обтекания бесконечного конуса сверхзвук, потоком идеального газа: OS — ударная волна; aa, dd — линии тока.

а нестационарное А. т.— в случае сильного точечного взрыва в среде, давление в к-рой много меньше давления, возникающего при взрыве. При обтекании бесконечного конуса (рис.) нельзя выделить характерный линейный размер. При растяжении или сжатии картины течения относительно вершины конуса О в произвольное число раз она не изменяется: все точки передвигаются вдоль лучей, выходящих из О, и вновь полученная картина течения ничем не отличается от исходной. Обтекание конуса является А. т. относительно изменения линейных размеров: все безразмерные хар-ки течения, напр. отношения давлений p2/p1 темп-р T2/T1, скоростей v2/v1, для двух произвольных точек 1 и 2 останутся неизменными при изменении линейных размеров путём растяжения или сжатия. Единственной геом. перем. величиной, определяющей параметры течения в любой меридиональной плоскости при заданном угле конуса 2b угле атаки d и Маха числе М набегающего потока, явл. полярный угол q между нек-рым лучом и направлением скорости потока.

К А. т. относятся обтекание сверхзвук, потоком плоского клина, непрерывное расширение газа при обтекании сверхзвук, потоком тупого угла (см. СВЕРХЗВУКОВОЕ ТЕЧЕНИЕ) и ряд др. течений. В этих случаях, как и при обтекании конуса, все параметры газа постоянны на лучах, выходящих из угл. точки, и изменяются лишь при изменении угл. координаты.

Все А. т. характеризуются тем, что их исследование можно свести к задаче с одной независимой переменной. Для нестационарных А. т. жидкостей и газов, когда параметры течения изменяются со временем, состояние течения в нек-рый момент времени t, характеризуемое распределением давлений, скоростей, темп-р в пр-ве, механически подобно состоянию течения при любом другом значении t; примером явл. распространение плоских, цилиндрич. и сферич. ударных волн в неогранич. пр-ве, когда единственной независимой переменной явл. отношение пространств. координаты (x или r) ко времени t.

К А. т. вязкого газа относятся нек-рые течения в пограничном слое и в свободной турбулентной струе, когда профили безразмерной скорости, темп-ры, концентрации изменяются подобным образом при изменении безразмерной геом. координаты.

В широком смысле под автомодельностью течения понимают независимость безразмерных параметров, характеризующих течение, от подобия критериев. Так, коэфф. лобового аэродинамич. сопротивления Cx (см. АЭРОДИНАМИЧЕСКИЕ КОЭФФИЦИЕНТЫ) можно считать автомодельными по числу Маха М и Рейнольдса числу Re, если в нек-ром диапазоне изменения этих критериев Cx от них не зависит. Автомодельность коэфф. Cx по числам М и Re существует для большинства тел, обтекаемых газом при очень больших значениях М (>8) или Re (>107) — см. рис. 1 и 2 в ст. (см. АЭРОДИНАМИЧЕСКИЕ КОЭФФИЦИЕНТЫ).

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

АВТОМОДЕЛЬНОЕ ТЕЧЕНИЕ

- течение жидкости (газа), к-рое остаётся механически подобным самому себе при изменении одного или неск. параметров, определяющих это течение. В механически подобных явлениях наряду с пропорциональностью геом. размеров соблюдается пропорциональность механич. величин - скоростей, давлений, сил и т. д. (см. Подобия теория).

А. т.- частный случай течения жидкости (газа), когда общая задача гидроаэромеханики сводится к системе безразмерных обыкновенных дифференц. ур-ний и граничных условий, зависящих от одной надлежащим образом выбранной безразмерной независимой переменной. Благодаря этому задача расчёта течения упрощается, и удаётся получить её численное, а в ряде случаев и аналитич. решение.

Так, при обтекании бесконечного конуса сверхзвуковым равномерным потоком идеального газа (рис. 1) нельзя выделить характерный линейный размер, поэтому при растяжении или сжатии картины течения относительно вершины конуса О в произвольное число раз картина не изменяется, т. е. остаётся подобной самой себе.

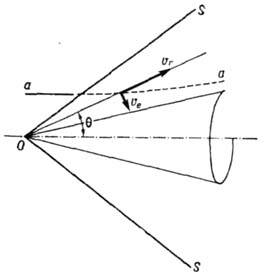
Рис. 1. Обтекание бесконечного конуса равномерным сверхзвуковым потоком идеального газа; OS - коническая ударная волна, аа- линия тока.

Все безразмерные характеристики течения - относит. скорости, давления и т. д. зависят от одной независимой геом. переменной - полярного угла 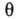. Обтекание конуса описывается системой из двух ур-ний -с граничными условиями на поверхности конуса и на присоединённой конич. ударной волне:

Здесь 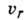, 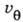- составляющие относит. скорости в полярной системе координат 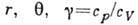- отношение уд. теплоёмкостей.

А. т. в ламинарном пограничном слое существуют лишь при нек-рых спец. законах изменения скорости U вне пограничного слоя, в частности при постоянной скорости U=const (пограничный слой на продольно обтекаемой бесконечной плоской пластине). Т. к. в рассматриваемом течении нет к.-л. характерной длины, то профили скорости в автомодельном пограничном слое в разл. поперечных сечениях x=const подобны друг другу и в безразмерных переменных представляются универсальной ф-цией 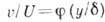, где у - расстояние по нормали к пластине, 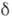- толщина пограничного слоя.

Безразмерная ф-ция тока 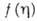в автомодельном пограничном слое удовлетворяет обыкновенному дифференц. ур-нию 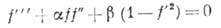с граничными условиями f=0, f '= 0 при и f'= 1 при . Здесь 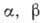- нек-рые постоянные, a h - безразмерная автомодельная переменная, пропорциональная . Аналогичные А. т. возможны и в пограничном слое, возникающем при свободной (естественной) конвекции.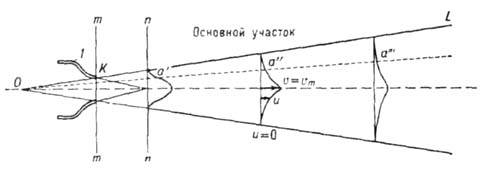

Рис. 2. Схема свободной турбулентной струи: О - полюс, I - сопло, m - т - сечение среза сопла, п - п - конец начального участка, KL - граница струи, 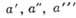- сходственные точки на профилях скорости.

А. т. возникает и в осн. участке турбулентной свободной струи (рис. 2), вытекающей из плоского или круглого сопла в неподвижную среду, т. к. в сходственных точках любых двух поперечных сечений безразмерные величины скорости (темп-ры, концентрации) одинаковы.

Для нестационарных А. т. состояние течения в нек-рый момент времени t, характеризуемое распределением давлений, скоростей, темп-р в пространстве, механически подобно состоянию течения при любом др. значении t. Такие течения образуются, напр., в случае сильного взрыва, а также при распространении в горючей смеси фронта пламени или детонации. В случае сферич. симметрии взрыв (поджигание смеси) происходит в точке, в случае цилиндрич. симметрии - вдоль прямой, а в случае плоских волн - вдоль плоскости. Если в момент t=0 мгновенно выделяется конечная энергия Е ₀ а нач. плотность газовой среды равна 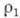, то введение безразмерной автомодельной переменной 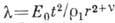(где r - расстояние от места взрыва, 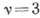-для сферич. волн, - для цилиндрических и 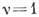-для плоских) позволяет свести задачу определения безразмерных давлений, скоростей, темп-р за взрывной (ударной) волной к решению системы обыкновенных дифференц. ур-ний с автомодельными граничными условиями на ударной волне.

В широком смысле под автомодельностью течения иногда понимают независимость безразмерных параметров, характеризующих течение, от подобия критериев. Так, коэфф. лобового аародинамич. сопротивления Сx (см. Аэродинамические коэффициенты )можно считать автомодельным по Маха числу М или Рейнольдса числу Re, если в нек-ром диапазоне их изменения Сх от них не зависит. Автомодельность коэфф. Сх по М и Re существует для большинства тел, обтекаемых газом, при больших М (М>8 )или достаточно больших Re(Re>10⁷).

Лит.: Седов Л. И., Методы подобия и размерности в механике, 9 изд., М., 1981; Xейз У.-Д., Пробстин Р.-Ф., Теория гиперзвуковых течений, пер. с англ., М., 1962; Шлихтинг Г., Теория пограничного слоя, М., 1974.

С. Л. Вишневецкий.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.