ПЕРЕКРЕСТНАЯ СИММЕТРИЯ

ПЕРЕКРЕСТНАЯ СИММЕТРИЯ

       

(кроссинг-симметрия), в квантовой теории поля (КТП) особая симметрия, связывающая амплитуду рождения к.-л. ч-цы с амплитудой поглощения соответствующей античастицы. В основе П. с. лежат два положения: 1) инвариантность ур-ний КТП относительно преобразований СРТ, т. е. относительно замены ч-цы на античастицу с противоположным по знаку импульсом и энергией (см. ТЕОРЕМА СРТ); 2) аналитич. св-ва амплитуд; амплитуда любого процесса явл. аналитич. ф-цией переменных sij=?i?j-pipj, где ?i(?j) и pi(pj) — энергия и импульс ч-цы i(j). П. с. означает, напр., что три процесса: a+b®c+d (I), a+d=®c+b= (II), a+c=®b=+d (III) описываются одной и той же аналитич. ф-цией переменных sab, sac и sad, но в разных областях их изменения. Так, если ч-цы а и с — g-кванты, a b и d — эл-ны, то процессами I, II, III в соответствующих областях .будут: g+e-®g+e-,g+е+®g+е+ — Комптона эффект на эл-не и позитроне; g+g®е++е- — рождение фотонами пары электрон-позитрон (или е++е- ®g+g — её двухфотонная аннигиляция).

П. с. явл. неотъемлемой составной частью метода дисперсионных соотношений и Редже полюсов метода.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ПЕРЕКРЁСТНАЯ СИММЕТРИЯ

(кроссинг-симметрия)- особый вид симметрии в квантовой теории поля, состоящий в том, что амплитудалюбого процесса не изменяется, если к.-л. частицы из начального и конечногосостояний поменять местами, заменив при этом частицы на античастицы. Была открыта в теории возмущений и на примере низшего порядка 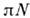-рассеянияизображена на рис. 1. Пример иллюстрирует отличие П. с. от СРТ -инвариантности(см. Теорема СРТ): нуклоны не затрагиваются П. с. В общем случаеП. с. следует из редукционных ф-л и доказана в аксиоматической квантовойтеории поля.

Рис. 1. Диаграммы Фейнмана перекрёстныхпроцессов упругого и -рассеяния;q,q' ( - q', - q) - начальные и конечные 4-импульсы 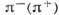- мезона.

Наиб. интересные выводы из П. с. следуютдля бинарного процесса a + bс+ d. Обозначим через s = ⁼ (Р _а + Р _ь)² квадратего полной энергии в системе центра инерции ( р _i -4-импульсчастицы i). Применяя П. с. к двум парам частиц (а, с) и (a, d),получим ещё два процесса, для к-рых роль s выполняют соответственнопеременные и = (р _b - p _с)² и t=( р _b - p_d)² (рис. 2).Величины (s, u,t )наз. манделстамовскими переменными, <а соответствующие им три процесса - s-, и- и t-каналами. П. с. утверждает, <что амплитуды трёх процессов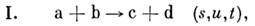

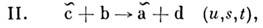
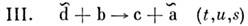
равны при указанных заменах манделстамовскихпеременных. Замены переменных следует понимать не формально, а как аналитическоепродолжение, напр. по переменной s для процесса I. При аналитич. <продолжении точка (s, и, t )из физ. области реакции I переходитв нефиз. область реакции II, что легко усматривается из вида замены (а, <с) в импульсном пространстве:

(p_a,p_b,p_c,p_d)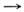(- p_c,p_b, - p_a,p_d).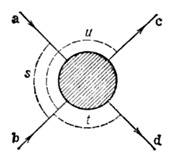

Рис. 2.

Возможность такого аналитич. продолжениябыла впервые доказана Н. Н. Боголюбовым при установлении дисперсионныхсоотношений (см. Дисперсионных соотношений метод )для -рассеянияпри фиксиров. значении переданного импульса. На основе спец. аксиоматики, <в к-рой ключевую роль играет принцип микропричинности Боголюбова, <было доказано существование единой аналитич. ф-ции комплексного переменного s, граничные значения к-рой представляют собой амплитуды перекрёстныхпроцессов. Область аналитичности и соответствие граничных значений амплитудамданы на рис. 3. Распространением представления о единой аналитич. ф-циина амплитуды, зависящие от неск. комплексных переменных, является Манделстамапредставление, к-рое ещё не доказано. Трудности доказательства аналитич. <свойств и конструктивного построения удовлетворяющих им амплитуд препятствуютпрямой эксперим. проверке П. с.

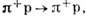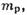
Рис. 3. Комплексная s-плоскость с разрезами, <соответствующими перекрёстным процессам (верхний берег правого разрезасоответствует физической области процесса нижний берег левого разреза - физической Области перекрёстного процесса 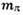- массы протона и 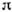-мезона).
Наиб. эффективно она была использованапри проверке дисперсионных соотношений в физике частиц. С её помощью поданным об эл.-магн. структуре протона предсказано существование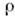 -мезона - резонансного состояния в системе двух пионов. П. с. активно применяетсяпри изучении асимптотич. свойств амплитуд процессов, в Редже полюсовметоде. Наиб. интересное использование она нашла в физике низких энергий. <Вместе с унитарности условием и предположением о важности малогочисла парциальных волн она позволила получить замкнутые системы ур-ний.

Лит.: Ширков Д. В., Серебряков В. <В., Мещеряков В. А., Дисперсионные теории сильных взаимодействий при низкихэнергиях, М., 1967; Бартон Г., Дисперсионные методы в теории поля, пер. <с англ., М., 1968; Ициксон К.,3юбер Ж.- Б., Квантовая теория поля, пер. <с англ., т. 1, М., 1984, гл. 5.

Б. <А. Мещеряков.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.