ОПТИЧЕСКИЙ РЕЗОНАТОР

ОПТИЧЕСКИЙ РЕЗОНАТОР

       

устройство, в к-ром могут возбуждаться стоячие или бегущие эл.-магн. волны оптич. диапазона. О. р. представляет собой совокупность неск. зеркал и явл. открытым резонатором, в отличие от большинства объёмных резонаторов, применяемых в диапазоне СВЧ. Для l<0,1 см использование закрытых объёмных резонаторов, имеющих размеры порядка l, затруднительно из-за малости их размеров и больших потерь энергии в станках. Использование же объёмных резонаторов с размерами l>l, также невозможно из-за возбуждения в них большого числа собств. колебаний, близких по частоте, в результате чего резонансные линии перекрываются, и резонансные св-ва практически исчезают. Однако оказалось, что при удалении части стенок объёмного резонатора б. ч. его собств. колебаний сильно затухает и лишь малая часть их (при надлежащей форме оставшихся стенок) затухает слабо. В результате спектр образовавшегося открытого О. р. сильно разрежен.

Простейшим О. р. явл. интерферометр Фабри — Перо, состоящий из двух плоских параллельных зеркал. Если допустить, что между этими зеркалами, расположенными на расстоянии L друг от друга, нормально к ним распространяется плоская волна, то в результате отражения её от зеркал в пр-ве между ними образуются стоячие волны. Условие резонанса имеет вид: L=ql/2, где q — целое число, наз. продольным индексом колебания (продольные моды). Собств. частоты О. р. образуют арифметич. прогрессию с разностью с/2L (эквидистантный спектр). В действительности из-за влияния краёв О. р. поле колебаний зависит от поперечных координат и характеризуется разл. поперечными индексами m и n, определяющими число осцилляции электрич. и магн. полей в поперечных направлениях и распределение токов на поверхности зеркал (рис. 1). Чем больше индексы m и n, тем число осцилляции больше и тем выше затухание колебания, обусловленное излучением в пр-во, т. е. в сущности дифракцией света на краях зеркал.

Рис. 1. Распределение токов, текущих по поверхности прямоуг. зеркала, для колебаний с индексами m=2 и n=1.

Резонансная кривая плоского О. р. имеет вид, изображённый на рис. 2. Поскольку коэфф. затухания растёт с увеличением m и n быстрее, чем частотный интервал между соседними колебаниями, то резонансные кривые, отвечающие большим m и n, перекрываются и соответствующие колебания не проявляются. Коэфф. затухания, вызванного излучением, зависит как от индексов m и n, так и от числа N зон Френеля, видимых на зеркале диаметром R из центра др. зеркала, находящегося от первого на расстоянии L: N=R2/2Ll. При N=1 остаётся 1 — 2 колебания, сопутствующие осн. колебанию.

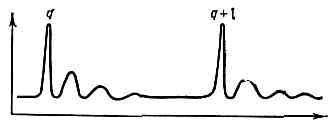Рис, 2. Резонансная кривая оптич. резонатора (схематически).

О. р. с плоскими зеркалами чувствительны к деформациям и перекосам зеркал, что ограничивает их применение. Этого недостатка лишены О. р. со сферич. зеркалами, в к-рых лучи, неоднократно отражаясь от вогнутых зеркал, не выходят за пределы огибающей поверхности — каустики. Поскольку волн. поле быстро убывает вне каустики при удалении от неё, излучение из сферич. О. р. с каустикой гораздо меньше, чем излучение из плоского О. р. Разрежение спектра в этом случае реализуется благодаря тому, что размеры каустики, ограничивающей поле, возрастают с ростом т и п. Для колебаний с большими m и n каустика оказывается расположенной вблизи края зеркал или вовсе не формируется, и эти колебания дают большой вклад в излучение. Такие сферич. О. р. наз. устойчивыми, т. к. параксиальный луч при отражении не уходит из приосевой области (рис. 3, а). Устойчивые О. р. применяются в газовых лазерах и др.

Иногда используются неустойчивые О. р., в к-рых внеш. каустика образоваться не может; луч, проходящий вблизи оси резонатора под малым углом к ней, после отражений неограниченно удаляется от оси. На рис. 3, б дана диаграмма устойчивости О. р. при разл. соотношениях между радиусами R1 и R2 зеркал и расстоянием L между ними. Незаштрихованные области соответствуют наличию каустик, заштрихованные — большому затуханию. Точки (на рисунке кружочки), соответствующие резонаторам с плоскими П и концентрическим К зеркалами, лежат на границе заштрихованных и незаштрихованных областей; С — софокусное, С' — плоское и вогнутое зеркала (половина софокусного резонатора). На границе между устойчивыми и неустойчивыми О. р. расположены софокусные О. р., в к-рых фокусы обоих зеркал (отстоящие на расстоянии R1/2 и R2/2 от соответствующего зеркала) совпадают, в т. ч. телескопический О. р., состоящий из малого выпуклого и большого вогнутого зеркал. Потери на излучение в неустойчивых О. р. для колебаний высших типов в них значительно больше, чем для осн. колебания. Это позволяет добиться одномодовой генерации лазера и связанной с ней высокой направленностью излучения.

Существуют различные дополнит. методы разрежения спектра (с е л е к ц и и м о д), связанные с измерением профиля краёв зеркал, с применением линз, системы связанных О. р. и др.

Рис. 3. a — образование каустики у резонатора со сферич. зеркалами; б — диаграмма устойчивости О. р.

Селекция продольных мод (имеющих одинаковое поперечное распределение поля) требует применения дисперсионных элементов (призм, дифракц. решёток, эталона Фабри — Перо).

Рис. 4. Кольцевые оптич. резонаторы: а, б, в — изотропные; г — анизотропный (1 — газоразрядные трубки, 2 — ячейка Фарадея, 3 — полуволновая пластина).

Но они вносят в О. р. большие потери и используются только в тех случаях, когда усиление активной среды лазера велико (напр., в лазерах на красителях). Селекция продольных мод возможна также при введении в О. р. анизотропных элементов (кристаллы с двойным лучепреломлением, оптически активные в-ва и др.). Для селекции поперечных мод применяется диафрагмирование пучка внутри О. р. При использовании кольцевых О. р. (рис. 4) осн. проблемой явл. уменьшение вз-ствия между встречными волнами. Для этого волны «разводят» по частоте с помощью невзаимных анизотропных элементов, а их поляризации стараются сделать ортогональными.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

ОПТИЧЕСКИЙ РЕЗОНАТОР

- совокупность неск. отражающих элементов, образующих открытый резонатор (в отличие от закрытых объёмных резонаторов, применяемых в диапазоне СВЧ). Для длин волн < 0,1 см использование закрытых резонаторов, имеющих размеры d~ затруднительно из-за малости d и больших потерь энергии в стенках. Использование же объёмных резонаторов с d > также невозможно из-за возбуждения в них большого числа собств. колебаний, близких по частоте, в результате чего резонансные линии перекрываются и резонансные свойства практически исчезают. В О. р. отражающие элементы не образуют замкнутой полости, поэтому большая часть его собств. колебаний сильно затухает и лишь малая часть их затухает слабо. В результате спектр образовавшегося О. р. сильно разрежен.
О. р. - резонансная система лазера, определяющаяспектральный и модовый состав лазерного излучения, а также его направленностьи поляризацию. От О. р. зависит заполненность активной среды лазера полемизлучения и, следовательно, снимаемая с неё мощность излучения и кпд лазера.
Простейшим О. р. является интерферометрФабри - Перо, состоящий из двух плоских параллельных зеркал. <Если между зеркалами, расположенными на расстоянии d друг от друга, <нормально к ним распространяется плоская волна, то в результате отраженияеё от зеркал в пространстве между ними образуются стоячие волны (собств. <колебания). Условие их образования где q - число полуволн, укладывающихся между зеркалами, наз. продольныминдексом колебания (обычно q~ 10⁴ - 10⁶).Собств. частоты О. р. образуют арифметич. прогрессию с разностью c/2d (эквидистантныйспектр). В действительности из-за дифракции на краях зеркал поле колебанийзависит и от поперечных координат, а колебания характеризуются также поперечнымииндексами т, п, определяющими число обращений поля в 0 приизменении поперечных координат. Чем больше т и п, тем вышезатухание колебаний, обусловленное излучением в пространство (вследствиедифракции света на краях зеркал). Моды с т = п =0 наз. продольными, <остальные - поперечными.
Т. к. коэф. затухания колебания растётс увеличением т и п быстрее, чем частотный интервал междусоседними колебаниями, то резонансные кривые, отвечающие большим т и п, перекрываются и соответствующие колебания не проявляются. Коэф. <затухания зависит также от числа N зон Френеля, видимых на зеркаледиам. R из центра др. зеркала, находящегося от первого на расстоянии d: (см. Френелязоны). При N ~ 1 остаётся 1 - 2 колебания, сопутствующих осн. <колебанию (q =1).

Двухзеркальные резонаторы. О. р. <с плоскими зеркалами чувствительны к деформациям и перекосам зеркал, чтоограничивает их применение. Этого недостатка лишены О. р. со сферич. зеркалами(рис. 1), в к-рых лучи, неоднократно отражаясь от вогнутых зеркал, не выходятза пределы огибающей поверхности - каустики. Поскольку волновоеполе быстро убывает вне каустики, излучение из сферич. О. р. с каустикойгораздо меньше, чем излучение из плоского О. р.

Рис. 1. Двухзеркальный резонатор.

Разрежение спектра в этом случае реализуетсяблагодаря тому, что размеры каустики растут с ростом т и n.Для колебаний с большими т и п каустика оказывается расположеннойвблизи края зеркал или вовсе не формируется. Сферич. О. р. с каустикойназ. устойчивыми, т. к. параксиальный луч при отражении не уходит из приосевойобласти (рис. 2, а). Устойчивые О. р. нечувствительны к небольшимсмещениям и перекосам зеркал, они применяются с активными средами, обладающиминебольшим усилением (10%на один проход). Для сред с большим усилением используются неустойчивыеО. р., в к-рых каустика образоваться не может; луч, проходящий вблизи осирезонатора под малым углом к ней, после отражений неограниченно удаляетсяот оси. На рис. 2( б )дана диаграмма устойчивости О. р. при разл. <соотношениях между радиусами R₁ и R₂ зеркал и расстоянием d между ними. Незаштрихованные области соответствуютналичию каустик, заштрихованные - их отсутствию. Точки, соответствующиерезонатору с плоскими (П) и концентрическими (К) зеркалами, лежат на границезаштрихованных областей. На границе между устойчивыми и неустойчивыми О. <р. расположен также конфокальный О. р. (R₁ = R₂= d). Из устойчивых О. р. наиб. часто используется полуконфокальный(R₁ =х R₂ = 2d), из неустойчивых - телескопическийО. р. (R₁+ R₂ = 2d). Потерина излучение в неустойчивых О. р. для колебаний высших типов значительнобольше, чем для осн. колебания. Это позволяет добиться одномодовой генерациилазера и связанной с ней высокой направленности излучения.

Рис. 2. Образование каустики( а )идиаграмма устойчивости двухзеркальных резонаторов ( б): знаком плюсотмечены области устойчивости; минусом - области неустойчивости; сплошныелинии - границы этих областей; П - резонатор с плоскими зеркалами; Конф.- конфокальный резонатор; К - концентрический резонатор; пунктир - линиятелескопических резонаторов.

Теория. Распределение электрич. поля . устойчивогоО. р. в плоскости, перпендикулярной оси О. р. (z), описывается выражением

Здесь Е ₀- коэф., определяющийамплитуду поля; Н _{т, <п} - полиномы Эрмита (см. Ортогональныеполиномы) т- йи n -й степеней: Н ₀ (х) =1, Н ₁(x)= 2х, Н₂( х) =4x² - 2, Н ₃ (х)=8 х ³ -12x; W - поперечный радиуспродольной моды (на расстоянии от оси О. р., равном W, плотностьэнергии продольной моды уменьшается в е раз). Зависимость W(z )имеет вид

где а z отсчитывается от т. н. перетяжки продольной моды, т. е. от той точкина оси резонатора, где её радиус имеет наим. значение, равное W₀ (рис.2, а). Расстояние от перетяжки до зеркала R₁

радиус продольной моды в перетяжке

Частотный спектр двухзеркального О. р. <задаётся условием

Распределение поля на зеркале показанона рис. 3. Т. к. частотный спектр двухзеркального О. р. вырожден (зависитлишь от суммы т + n, но не от каждого из индексов в отдельности),то Е(х, <у )может отличаться от (1). Конкретный вид распределенийзависит от слабых возмущающих действий со стороны диафрагм или др. объектовв области, занимаемой пучком. В частности, при осевой симметрии возможныраспределения полей (рис. 4), описываемые в цилиндрич. координатах(r,,z )выражением

Здесь l, p - индексы колебания, <определяющие число обращений поля в 0 при изменении r и W(z)- радиус продольной моды;- обобщённый полином Лагерра:

Спектр О. р. при осевой симметрии определяетсясоотношением (2), где ( т+ п+ 1) следует заменить на (2р+l+1).

Рис. 3. Распределение поля на зеркале припрямоугольной симметрии.

Рис. 4. Распределение поля на зеркале приосевой симметрии; * соответствует распределению поля при сложении двухортогонально поляризованных мод.

Составной резонатор. Кроме зеркал О. р. <часто содержит т. н. активные элементы (пластинки, линзы и др.). СоставнойО. р. может работать в двух режимах в зависимости от того, используетсяили теряется излучение, отражённое от промежуточных поверхностей. Еслиотражённое излучение используется, то О. р. наз. согласованным. Каждаячасть согласованного О. р., заключённая между двумя соседними поверхностямираздела, может рассматриваться как отд. резонатор, причём поперечные модыэтих резонаторов подбирают так, чтобы они совпадали на границах раздела. <Условие согласования (рис. 5) имеет вид

Рис. 5.

Согласованный О. р. обладает неэквидистантнымспектром и может быть использован для разрежения продольного спектра О. <р. (см. ниже).
Важной проблемой в случае составного О. <р. является эфф. заполнение активной среды лазера полем выбранной моды. <Если составной О. р. обладает осью или плоскостью симметрии, то продольнаямода (как и у двухзеркального О, р.) является гауссовым пучком (см. Квазиоптика). Егопрохождение через оптич. элементы описывается матрицами этих элементов(см. Матричные методы в оптике), а прохождение через О. р. описываетсяматрицей, являющейся произведением матриц составляющих его оптич. элементов. <При этом комплексный параметр гауссова пучка q определяется ур-нием

Cq² + (D - A)q - B = 0.

Коэф. А, В, С, D образуют матрицуО. р. Это ур-ние, а также соотношения R = [Re(^l/q)]^-l,=[kIm(¹/q)]^-1 позволяют определить поперечныйрадпус пучка и радиус кривизны волнового фронта R в любом сечении резонатора.

Селекция продольных мод. Для разрежения(селекции) продольных мод, имеющих одинаковое поперечное распределениеполя, но отличающихся частотой, используются резонаторы, содержащие дисперсионныеэлементы (призмы, дифракц. решётки, интерферометры и др.). В частности, <в качестве дисперсионного элемента применяют дополнит. О. р., связанныес основным и образующие т. н. эквивалентное зеркало, коэф. отражения к-рогоrзависит от частоты v. Для удаления из спектра одной из продольныхмод наиб. пригоден линейный трёхзеркальный О. р. (рис. 6, а), длявыделения в спектре одной продольной моды - резонатор Фокса - Смита (рис.6, б) и Т-образный (рис. 6, в). В нек-рых случаях удобен О. <р. Майкельсона (рис. 6, г).

Рис. 6. Различные типы связанных резонаторов(I) и зависимость коэффициента отражения эквивалентного зеркала 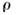отчастоты v(II).

В лазерах на красителях применяется комбинациядифракц. решётки и интерферометра Фабри - Перо (рис. 7). При этом интерферометрвыделяет одну продольную моду, а решётка предотвращает генерацию на др. <порядках интерферометра. Линзы Л ₁ и Л ₂, образующиет. н. телескоп, согласуют узкий пучок, проходящий через активную средуА, с широким пучком, попадающим на интерферометр и решётку .Активная средав таком О. р. играет также роль диафрагмы, выделяющей осн. поперечную моду. <Такие О. р. позволили создать перестраиваемые в широком диапазоне одночастотные лазерына красителях.

Рис. 7. Резонатор, содержащий дисперсионныеэлементы (используемый в лазерах на красителях). А - кювета с активнойсредой; З - непрозрачное или частично прозрачное зеркало; И - интерферометрФабри - Перо; Д - дифракционная решётка.

Селекция поперечных мод основана на различиив распределении полей поперечных мод с разными т и п. Т. <к. обычно требуется выделить осн. моду, к-рая имеет мин. угл, расходимость, <гауссово распределение и мин. протяжённость в поперечном направлении, топрименяется диафрагмирование пучка внутри О. р. Радиус диафрагмы ориентировочнодолжен быть равен поперечному радиусу моды, следующей за основной. Приэтом потери всех мод, кроме основной, сильно увеличиваются.
При селекции поперечных мод необходимо, <чтобы оставшаяся единств. мода эффективно заполняла активную среду. Поэтомуважны границы зон устойчивости (рис. 2,6), где поперечные размерымод увеличиваются: 1) радиус моды увеличивается во всём объёме, если расстояние . между зеркалами постоянно, а радиусы крпвизны зеркал R_l и R₂ (приэтом сильно увеличивается чувствительность резонатора к разъюстировкам);2) радиус моды увеличивается на 1-м зеркале и уменьшается на 2-м, если dR₁(R₂R₁); 3) радиус моды увеличивается на 2-м зеркале и уменьшаетсяна 1-м, если dR₂;4) радиус моды увеличивается на обоих зеркалах и уменьшаетсяв области их центров кривизны, если d(R₁ + R₂).
При необходимости выделения к.-л. высшеймоды на нулевой линии распределения поля этой моды помещают тонкую рассеивающуюнить, к-рая не оказывает влияния на избранную моду и подавляет др. моды, <не обращающиеся в 0 на этой линии.
Резонаторы с анизотропными элементами. <Поляризация лазерного излучения определяется т. н. анизотропными элементами, <находящимися в О. р. Такими элементами являются двулучепреломляющие пластины, поляризаторы, вещества, обладающие оптической активностью, и др., а такжепластины Брюстера и диэлектрич. зеркала при наклонном падении на них излучения. <Определение поляризации производится матричным методом Джонса. При этомполяризац. матрица всего О. р. является произведением матриц входящих внего элементов, расположенных в том порядке, в к-ром через эти элементыпроходит излучение начиная с того места, где требуется определить состояниеполяризации. Собств. векторы поляризац. матрицы являются векторами Джонса Е (Е _х,Е _у) полей, генерируемых в О. р. <Степень поляризации е и направление гл. оси эллипса поляризации а определяютсясоотношениями

где R = |Е _х| / |Е _у|,=arcig(E_y/E_x).

Модули собств. значений матрицы Джонсаопределяют потери О. р., обусловленные поляризаторами, а фазы собств. значений- поляризац. поправки к частотам соответствующих мод. Подбирая анизотропныеэлементы, можно добиться требуемого состояния поляризации. Учитывая, чтообычно анизотропные элементы обладают заметной дисперсией, можно использоватьих также для разрежения продольного спектра.

Кольцевые резонаторы. Спектр собств. <частот кольцевого О. р., образованного тремя одинаковыми сферич. зеркаламирадиуса R, расположенными в вершинах равностороннего треугольникасо стороной а (рис. 8), определяется соотношением

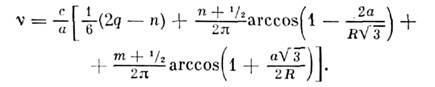
Рис. 8. Кольцевые оптические резонаторы.

Перетяжки мод находятся на серединах сторонтреугольника; поперечные протяжённости мод в области перетяжки в плоскостиосевого контура равны:

Если у резонатора лишь одно зеркало сферическое, <а два плоских (рис. 8,6), то его спектр определяется соотношением

Поперечные протяжённости мод в областиперетяжки, к-рая находится на середине стороны треугольника, противолежащейсферич. зеркалу в плоскости резонатора, равны:

Оптич. система, образующая О. р. с неплоскимконтуром, напр. система из 4 зеркал, расположенных в вершинах тетраэдра(рис. 8, в), характеризуется тем, что изображение того или иногопредмета, построенное с помощью этой системы, повёрнуто относительно самогопредмета на нек-рый свойственный этой системе угол. Для тетраэдра этотугол равен где -углы между соседними плоскостями падения лучей на зеркала (грани тетраэдра),к-рые отсчитываются так, что тетраэдр лежит внутри угла. Продольной модойО. р. с неплоским контуром является пучок, у к-рого гл. оси эллиптич. амплитудногораспределения развёрнуты на нек-рый угол относительно гл. линий кривизныволнового фронта. Благодаря этому амплитудное распределение при распространениипучка в свободном пространстве испытывает поворот, к-рый компенсирует поворот, <обусловленный объёмным расположением зеркал. Кольцевые О. р. с неплоскимконтуром применяются, напр., в лазерных гироскопах. Они позволяют, <в частности, избавиться от анизотропии, свойственной кольцевым О. р. сплоским контуром.

Неустойчивые резонаторы обладаютвысокими потерями на излучение во внеш. пространство (см. выше). Потеривозрастают с увеличением т и п, благодаря этому неустойчивыеО. р. обеспечивают одномодовую (по т и п )генерацию. Достоинствомнеустойчивых О. р. является большая поперечная протяжённость осн. моды, <вследствие чего они могут быть использованы с активными средами большогопоперечного сечения. Вывод энергии из неустойчивого О. р., как правило, <осуществляется не сквозь зеркала, как в устойчивых О. р., а за краями одногоиз зеркал. В неустойчивых О. р. существенную (отрицат.) роль играет волна, <отражённая от края зеркала и сходящаяся к оси О. р. Для уменьшения такогоотражения применяют сглаживание края зеркала, к-рому придаётся звездообразнаяформа, скругляются края и т. п.
Осн. мода неустойчивого О. р. образованадвумя сферич. волнами, распространяющимися между зеркалами навстречу другдругу. В случае телескопич. неустойчивого О. р. (рис. 9) одна из волн можетбыть плоской. Центр сферич. волны лежит на расстоянии х = R₂/2за выпуклым зеркалом с радиусом кривизны R₂. Вогнутоезеркало должно обладать при этом радиусом кривизны |R₁| =R₂ + 2d (R_l< 0). При достаточно большихпоперечных размерах 1-го зеркала пучок излучения кольцевой формы выводитсяв сторону выпуклого зеркала с волновым фронтом, близким к плоскому.
Неустойчивые О. р. с вращением поля образуютсяде-фокусирующей системой зеркал, расположенных в вершинах неплоского многоугольника. <Однако наиб. важны О. р., образуемые двумя двугранными уголковыми отражателями(рис. 10), рёбра к-рых развёрнуты друг относительно друга на угол .Если одна или неск. граней отражателей являются выпуклыми, то О. р. неустойчив.

Рис. 9. Неустойчивый телескопический резонатор.

Рис. 10. Линейный резонаторс вращением поля, образованный уголковыми отражателями.

Поле при полном обходе такого резонатораиспытывает поворот на угол Достоинством неустойчивого О. р. с вращением поля является возможностьвывода излучения в виде не кольцевого пучка, как в обычном неустойчивомО. р., а односвязного компактного пучка (рис. 11).

Рис. 11. Вывод энергии в виде компактногоодносвязного пучка из неустойчивого резонатора с вращением поля на АС- ребро уголкового отражателя зеркала, вблизи которого выводится пучокизлучения (заштрихован), НН' - обрез того же зеркала, GG' - ребровторого уголкового отражателя.

Лит.: Вайнштейн Л. А., Открытыерезонаторы и открытые волноводы, М., 1966; Ананьев Ю. А., Оптические резонаторыи проблема расходимости лазерного излучения, М., 1979; Справочник по лазерам, <пер. с англ., под ред. А. М Прохорова, т. 2, М., 1978, гл. 22, 23; КарловН. В., Лекции по квантовой электронике, 2 изд., М., 1988.

В. П. Быков

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.