МОЛЕКУЛЯРНЫЕ СПЕКТРЫ

МОЛЕКУЛЯРНЫЕ СПЕКТРЫ

       

спектры испускания, поглощения и комбинационного рассеяния света (КРС), принадлежащие свободным или слабо связанным между собой молекулам. Типичные М. с.— полосатые, они наблюдаются в виде совокупности более или менее узких полос в УФ, видимой и ИК областях спектра; при достаточной разрешающей способности спектральных приборов мол. полосы распадаются на совокупность тесно расположенных линий. Структура М. с. различна для разл. молекул и усложняется с увеличением числа атомов в молекуле. Видимые и УФ спектры весьма сложных молекул сходны между собой и состоят из немногих широких сплошных полос. М. с. возникают при квантовых переходах между уровнями энергии ?' и ?" молекул согласно соотношению:

hv=?'-?", (1)

где hv — энергия испускаемого или поглощаемого фотона частоты v. При КРС hv равна разности энергий падающего и рассеянного фотонов. М. с. гораздо сложнее атомных спектров, что определяется большей сложностью внутр. движений в молекуле, т. к. кроме движения эл-нов относительно двух и более ядер в молекуле происходит колебат. движение ядер (вместе с окружающими их внутр. эл-нами) около положения равновесия и вращат. движения её как целого. Электронному, колебат. и вращат. движениям молекулы соответствуют три типа уровней энергии ?эл, ?кол и ?вр н три типа М. с.

Согласно квант. механике, энергия всех видов движения в молекуле может принимать только определённые значения (квантуется). Полная энергия молекулы ? приближённо может быть представлена в виде суммы квантованных значений энергий, соответствующих трём видам её внутр. движений:

?»?эл +?кол+?вр, (2) причём по порядку величины

?эл:?кол:?вр = 1: ?m/M:m/M, (3)

где т — масса эл-на, а М имеет порядок массы ядер атомов в молекуле, т. <е. m/M=10-5—10-3, следовательно:

?эл -> ?кол ->?вр. (4) Обычно ?эл порядка неск. эВ (сотен кДж/моль), ?кол = 10-2—10-1 эВ, ?вр=10-5—10-3 эВ.

Система уровней энергии молекулы характеризуется совокупностями далеко отстоящих друг от друга электронных уровней энергии (разл. ?эл при ?кол=?вр=0). расположенных значительно ближе друг к другу колебательных уровней (разл. ?кол при заданном ?эл и ?вр=0) и ещё более близких друг к другу вращательных уровней (значения ?вр при заданных ?эл и ?кол).

Электронные уровни энергии а к б на рис. 1 соответствуют равновесным конфигурациям молекулы. Каждому электронному состоянию соответствует определённая равновесная конфигурация и определённое значение ?эл; наименьшее значение соответствует осн. электронному состоянию (осн. электронный уровень энергии молекулы).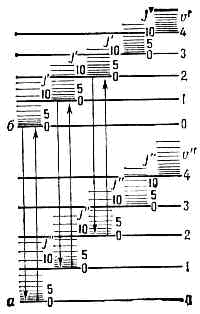

Рис. 1. Схема Уровней энергии двухатомной молекулы, а и б — электронные уровни; v' и v" — квант. числа колебат. уровней; J' и J" — квант. числа вращат. уровней.

Набор электронных состояний молекулы определяется св-вами её электронной оболочки. В принципе значения ?эл можно рассчитать методами квант. химии, однако эта задача решается только приближённо и для сравнительно простых молекул. Важную информацию об электронных уровнях молекул (их расположении и их хар-ках), определяемую её хим. строением, получают, изучая М. с.

Весьма важная хар-ка электронного уровня энергии — значение квантового числа 5, определяющего абс. величину полного спинового момента всех эл-нов. Химически устойчивые молекулы имеют, как правило, чётное число эл-нов, и для них 5 = 0, 1, 2, . . .; для осн. электронного уровня типично 5=0, для возбуждённых — 5 = 0 и 5=1. Уровни с S=0 наз. синглетными, с S=1 — триплетными (т. к. их мулътиплетность c=2S+1=3).

В случае двухатомных и линейных трёхатомных молекул электронные уровни характеризуются значением квант. числа Л, определяющего абс. величину проекции полного орбитального момента всех эл-нов на ось молекулы. Уровни с L=0, 1, 2, ... обозначаются соответственно S, П, D, . . ., а и указывается индексом слева вверху (напр., 3S, 2П). Для молекул, обладающих центром симметрии (напр., СО2, СН6), все электронные уровни делятся на чётные и нечётные (g и u соответственно) в зависимости от того, сохраняет или нет определяющая их волновая функция знак при обращении в центре симметрии.

Колебательные уровни энергии можно найти квантованием колебат. движения, к-рое приближённо считают гармоническим. Двухатомную молекулу (одна колебат. степень свободы, соответствующая изменению межъядерного расстояния r) можно рассматривать как гармонич. осциллятор, квантование к-рого даёт равноотстоящие уровни энергии:

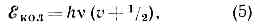где v — осн. частота гармонич. колебаний молекулы, v=0, 1, 2, . . .— колебат. квант. число.

Для каждого электронного состояния многоатомной молекулы, состоящей из N?3 атомов и имеющей f Колебат. степеней свободы (f=3N-5 и f=3N-6 для линейных и нелинейных молекул соответственно), получается / т. н. нормальных колебаний с частотами vi(ill, 2, 3, . . ., f) и сложная система колебат. уровней энергии:

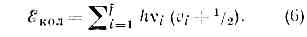Набор частот норм. колебаний в осн. электронном состоянии явл. важной хар-кой молекулы, зависящей от её хим. строения. В определённом норм. колебании участвуют либо все атомы молекулы, либо их часть; атомы совершают гармонич. колебания с одинаковой частотой vi, но с разл. амплитудами, определяющими форму колебания. Норм. колебания разделяют по форме на валентные (изменяются длины хим. связей) и деформационные (изменяются углы между хим. связями — валентные углы). Для молекул низшей симметрии (см. СИММЕТРИЯ МОЛЕКУЛЫ) f=2 и все колебания невырожденные; для более симметричных молекул имеются дважды и трижды вырожденные колебания, т. е. пары и тройки совпадающих по частоте колебаний.

Вращательные уровни энергии можно найти квантованием вращат. движения молекулы, рассматривая её как тв. тело с определёнными моментами инерции. В случае двухатомной или линейной трёхатомной молекулы её энергия вращения ?вр=М2/2I, где I — момент инерции молекулы относительно оси, перпендикулярной оси молекулы, а М — вращат. момент кол-ва движения. Согласно правилам квантования,

M2=(h/4pi2)J(J+1),

где f=0, 1,2,. . .— вращательное квант. число; для ?вр получаем:

?вр=(h2/8pi2I)J(J+1) = hBJ(J+1), (7)

где вращат. постоянная В=(h/8piI2)I

определяет масштаб расстояний между уровнями энергии, уменьшающийся с увеличением масс ядер и межъядерных расстояний.

Разл. типы М. с. возникают при разл. типах переходов между уровнями энергии молекул. Согласно (1) и (2):

D?=?'-?"==D?эл+D?кол+D?вр,

причём аналогично (4) D?эл->D?кол->D?вр. При D?эл?0 получаются электронные М. с., наблюдаемые в видимой и УФ областях. Обычно при D??0 одновременно D?кол?0 и D?вр?0; разл. D?кол при заданном D?эл соответствуют разл. колебат. полосы (рис. 2), а разл. D?вр при заданных D?эл и D?кол отд. вращат. линии, на к-рые распадаются колебат. полосы (рис. 3).

Рис. 2. Электроино-колебат. спектр молекулы N2 в близкой УФ области; группы полос соответствуют разл. значениям Dv= v'-v".

Совокупность полос с заданным D?эл (соответствующих чисто электронному переходу с частотой nэл=D?эл/h) наз. системой полос; полосы обладают разл. интенсивностью в зависимости от относит. вероятностей переходов (см. КВАНТОВЫЙ ПЕРЕХОД).

Рис. 3. Вращат. расщепление электронно-колсбат. полосы 3805,0 ? молекулы N2.

Для сложных молекул полосы одной системы, соответствующие данному электронному переходу, обычно сливаются в одну широкую сплошную полосу; могут накладываться друг на друга и неск. таких полос. Характерные дискретные электронные спектры наблюдаются в замороженных р-рах органич. соединений.

Электронные (точнее, электронно-колебательно-вращательные) спектры изучаются с помощью спектральных приборов со стеклянной (видимая область) и кварцевой (УФ область, (см. УЛЬТРАФИОЛЕТОВОЕ ИЗЛУЧЕНИЕ)) оптикой. При D?эл = 0, а D?кол?0 получаются колебат. М. с., наблюдаемые в ближней ИК области обычно в спектрах поглощения и КРС. Как правило, при заданном D?кол D?вр ?0 и колебат. полоса распадается на отд. вращат. линии. Наиболее интенсивны в колебат. М. с. полосы, удовлетворяющие условию Dv=v'- v"=1 (для многоатомных молекул Dvi=v'i- v"i=1 при Dvk=V'k-V"k=0; здесь i и k определяют разл. нормальные колебания). Для чисто гармонич. колебаний эти правила отбора выполняются строго; для ангармонич. колебаний появляются полосы, для к-рых Dv>1 (обертоны); их интенсивность обычно мала и убывает с увеличением Dv. Колебат. М. с. (точнее, колебательно-вращательные) изучают с помощью ИК спектрометров и фурье-спектрометров, а спектры КРС — при помощи светосильных спектрографов (для видимой области) с применением лазерного возбуждения. При D?эл=0 и D?кол=0 получаются чисто вращат. спектры, состоящие из отд. линий. Они наблюдаются в спектрах поглощения в далёкой ИК области и особенно в микроволновой области, а также в спектрах КРС. Для двухатомных, линейных трёхатомных молекул и достаточно симметричных нелинейных молекул эти линии равноотстоят (в шкале частот) друг от друга.

Чисто вращат. М. с. изучают с помощью ИК спектрометров со спец. дифракц. решётками (эшелеттами), фурье-спектрометров, спектрометров на основе лампы обратной волны, микроволновых (СВЧ) спектрометров (см. СУБМИЛЛИМЕТРОВАЯ СПЕКТРОСКОПИЯ, МИКРОВОЛНОВАЯ СПЕКТРОСКОПИЯ), а вращат. спектры КРС — с помощью светосильных спектрометров.

Методы молекулярной спектроскопии, основанной на изучении М. с., позволяют решать разнообразные задачи химии. Электронные М. с. дают информацию об электронных оболочках, возбуждённых уровнях энергии и их хар-ках, об энергии диссоциации молекул (по схождению уровней энергии к границе диссоциации). Исследование колебат. спектров позволяет находить характеристические частоты колебаний, соответствующие наличию в молекуле определённых типов хим. связей (напр., двойных и тройных связей С—С, связей С—Н, N—Н для органич. молекул), определять пространств. структуру, различать цис- и транс-изомеры (см. ИЗОМЕРИЯ МОЛЕКУЛ). Особо широкое распространение получили методы инфракрасной спектроскопии — одни из наиболее эффективных оптич. методов изучения строения молекул. Наиболее полную информацию они дают в сочетании с методами спектроскопии КСР. Исследование вращат. спектров, а также вращат. структуры электронных и колебат. М. с. позволяет по найденным из опыта моментам инерции молекул находить с большой точностью параметры равновесных конфигураций — длины связей и валентные углы. Для увеличения числа определяемых параметров исследуют спектры изотопич. молекул (в частности, молекул, в к-рых водород заменён дейтерием), имеющих одинаковые параметры равновесных конфигураций, но разл. моменты инерции.

М. с. применяются также в спектральном анализе для определения состава в-ва.

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

МОЛЕКУЛЯРНЫЕ СПЕКТРЫ

- спектры поглощения, испускания или рассеяния, возникающие при квантовых переходах молекул из одного энергетич. состояния в другое. M. с. определяются составом молекулы, её структурой, характером хим. связи и взаимодействием с внеш. полями (и, следовательно, с окружающими её атомами и молекулами). Наиб. характерными получаются M. с. разреженных молекулярных газов, когда отсутствует уширение спектральных линий давлением: такой спектр состоит из узких линий с доп-леровской шириной.

Рис. 1. Схема уровней энергии двухатомной молекулы: a и б -электронные уровни; u' и u " - колебательные квантовые числа; J' и J " - вращательные квантовые числа.

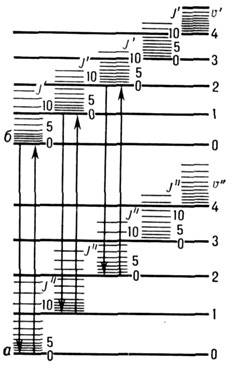
В соответствии с тремя системами уровней энергии в молекуле - электронной, колебательной и вращательной (рис. 1), M. с. состоят из совокупности электронных, колебат. и вращат. спектров и лежат в широком диапазоне эл.-магн. волн - от радиочастот до рентг. области спектра. Частоты переходов между вращат. уровнями энергии обычно попадают в микроволновую область (в шкале волновых чисел 0,03-30 см ^-1), частоты переходов между колебат. уровнями -в ИК-обла-сть (400-10 000 см ^-1), а частоты переходов между электронными уровнями - в видимую и УФ-области спектра. Это разделение условное, т. к. часто вращат. переходы попадают и в ИК-область, колебат. переходы - в видимую область, а электронные переходы - в ИК-область. Обычно электронные переходы сопровождаются и изменением колебат. энергии молекулы, а при колебат. переходах изменяется и вращат. энергия. Поэтому чаще всего электронный спектр представляет собой системы электронно-колебат. полос, причём при высоком разрешении спектральной аппаратуры обнаруживается их вращат. структура. Интенсивность линий и полос в M. с. определяется вероятностью соответствующего квантового перехода. Наиб. интенсивные линии соответствуют переходу, разрешённому отбора правилами. К M. с. относят также оже-спектры и рентг. спектры молекул (в статье не рассматриваются; см. Оже-эффект, Оже-спектроскопия, Рентгеновские спектры, Рентгеновская спектроскопия).

Электронные спектры. Чисто электронные M. с. возникают при изменении электронной энергии молекул, если при этом не меняются колебат. и вращат. энергии. Электронные M. с. наблюдаются как в поглощении (спектры поглощения), так и в испускании (спектры люминесценции). При электронных переходах обычно изменяется электрич. дипольный момент молекулы. Эле-ктрич. дипольный переход между электронными состояниями молекулы типа симметрии Г ' и Г " (см. Симметрия молекул )разрешён, если прямое произведение Г ' Г " содержит тип симметрии, по крайней мере одной из компонент вектора дипольного момента d. B спектрах поглощения обычно наблюдают переходы из основного (полносимметричного) электронного состояния в возбуждённые электронные состояния. Очевидно, что для осуществления такого перехода типы симметрии возбуждённого состояния и дипольного момента должны совпадать. T. к. электрич. дипольный момент не зависит от спина, то при электронном переходе спин должен сохраняться, т. е. разрешены только переходы между состояниями с одинаковой мультиплетностью (интер-комбинац. запрет). Это правило, однако, нарушается

для молекул с сильным спин-орбитальным взаимодействием, что приводит к интеркомбинационным квантовым переходам. В результате таких переходов возникают, напр., спектры фосфоресценции, к-рые соответствуют переходам из возбуждённого триплет-ного состояния в осн. синглетное состояние.

Молекулы в разл. электронных состояниях часто имеют разную геом. симметрию. В таких случаях условие Г ' Г " Г _d должно выполняться для точечной группы низкосимметричной конфигурации. Однако при использовании перестановочно-инверсионной (ПИ) группы такая проблема не возникает, т. к. ПИ группа для всех состояний может быть выбрана одинаковой.

Для линейных молекул симметрии С _ху тип симметрии дипольного момента Г _d = S⁺(d_z )-P(d_x, d_y), поэтому для них разрешены только переходы S⁺ - S⁺, S^- -S^-, П - П и т. д. с дипольным моментом перехода, направленным по оси молекулы, и переходы S⁺ - П, П - D и т. д. с моментом перехода, направленным перпендикулярно оси молекулы (обозначения состояний см. в ст. Молекула).

Вероятность В электрич. дипольного перехода с электронного уровня т на электронный уровень п, просуммированная по всем колебательно-вращат. уровням электронного уровня т, определяется ф-лой:

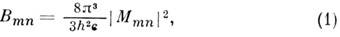
где

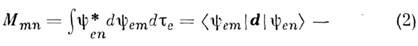
матричный элемент дипольного момента для перехода n - m,y _еп и y_em - волновые ф-ции электронов. Ин-тогральный коэф. поглощения, к-рый можно измерить экспериментально, определяется выражением

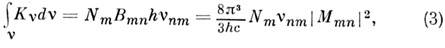
где N_m - число молекул в нач. состоянии m, v_nm- частота перехода т 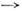п. Часто электронные переходы характеризуются силой осциллятора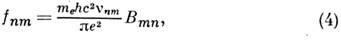

где е и т _е- заряд и масса электрона. Для интенсивных переходов f_nm ~1. Из (1) и (4) определяется ср. время жизни возбуждённого состояния:

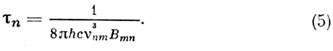
Эти ф-лы справедливы также и для колебат. и вращат. переходов (в этом случае следует переопределить матричные элементы дипольного момента). Для разрешённых электронных переходов обычно коэф. поглощения на неск. порядков больше, чем для колебат. и вращат. переходов. Иногда коэф. поглощения достигает величины ~10³-10⁴ см ^-1 атм ^-1, т. е. электронные полосы наблюдаются при очень низких давлениях (~10^-3- 10^-4 мм рт. ст.) и малых толщинах (~10-100 см) слоя вещества.

Колебательные спектры наблюдаются при изменении колебат. энергии (электронная и вращат. энергии при этом не должны меняться). Нормальные колебания молекул обычно представляют как набор невзаимодействующих гармонич. осцилляторов. Если ограничиться только линейными членами разложения дипольного момента d (в случае спектров поглощения) или поляризуемости a (в случае комбинац. рассеяния) по нормальным координатам Q_k, то разрешёнными колебат. переходами считаются только переходы с изменением одного из квантовых чисел u_k на единицу. Таким переходам соответствуют осн. колебат. полосы, они в колебат. спектрах наиб. интенсивны.

Осн. колебат. полосы линейной многоатомной молекулы, соответствующие переходам из осн. колебат. состояния, могут быть двух типов: параллельные (||) полосы, соответствующие переходам с дипольным моментом перехода, направленным по оси молекулы, и перпендикулярные (1) полосы, отвечающие переходам с дипольным моментом перехода, перпендикулярным оси молекулы. Параллельная полоса состоит только из R- и Р -ветвей, а в перпендикулярной полосе раз-

решена также и Q -ветвь (рис. 2). Спектр осн. полос поглощения молекулы типа симметричного волчка также состоит из || и | полос, но вращат. структура этих полос (см. ниже) более сложная; Q- ветвьв || полосе также не разрешена. Разрешённые колебат. полосы обозначают v_k. Интенсивность полосы v_k зависит от квадрата производной ( дd/дQ _к)² или ( дa/ дQ_k)². Если полоса соответствует переходу из возбуждённого состояния на более высокое, то её наз. горячей.

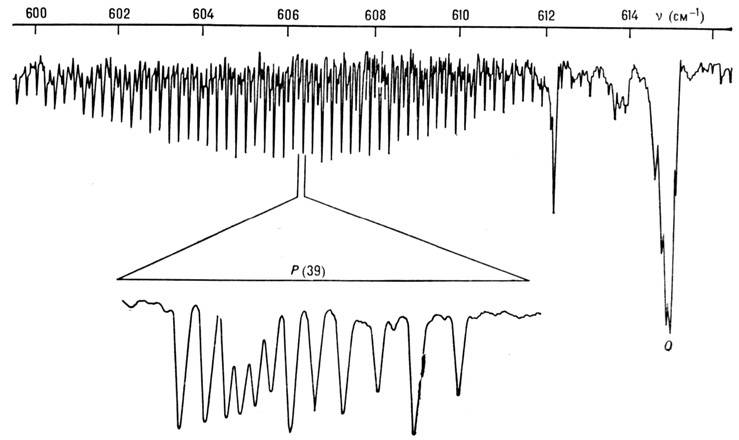
Рис. 2. ИК-полоса поглощения v₄ молекулы SF₆, полученная на Фурье-спектрометре с разрешением 0,04 см ^-1; нише показана тонкая структура линии Р(39), измеренная на диодном лазерном спектрометре с разрешением 10^-4 см ^-1.

При учёте энгармонизма колебаний и нелинейных членов в разложениях d и a по Q_k становятся вероятными и переходы, запрещённые правилом отбора по u_k. Переходы с изменением одного из чисел u_k на 2, 3, 4 и т. д. наз. обертонными (Du_k =2 - первый обертон, Du_k =3 - второй обертон и т. д.). Если при переходе изменяются два или более из чисел u_k, то такой переход наз. комбинационным или суммарным (если все u _к увеличиваются) и разностным (если нек-рые из u_k уменьшаются). Обертонные полосы обозначаются 2v_k, 3v_k, ..., суммарные полосы v_k + v_l, 2v_k + v_l и т. д., а разностные полосы v_k - v_l, 2v_k - e_l и т. д. Интенсивности полос 2u_k, v_k + v_l и v_k - v_l зависят от первых и вторых производных d по Q_k. (или a по Q_k) и кубич. коэффициентов ангармонизма потенц. энергии; интенсивности более высоких переходов зависят от коэф. более высоких степеней разложения d (или a) и потенц. энергии по Q_k.

Для молекул, не имеющих элементов симметрии, разрешены все колебат. переходы как при поглощении энергии возбуждения, так и при комбинац. рассеянии света. Для молекул, имеющих центр инверсии (напр., CO₂, C₂H₄ и др.), переходы, разрешённые в поглощении, запрещены для комбинац. рассеяния, и наоборот (альтернативный запрет). Переход между колебат. уровнями энергии типов симметрии Г ₁ и Г ₂ разрешён в поглощении, если прямое произведение Г ₁ 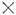Г ₂ содержит тип симметрии дипольного момента, и разрешён в комбинац. рассеянии, если произведение Г ₁

Г ₂ содержит тип симметрии тензора поляризуемости. Это правило отбора приближённое, т. к. оно не учитывает взаимодействия колебат. движения с электронным и вращат. движениями. Учёт этих взаимодействий приводит к возникновению полос, запрещённых согласно чисто колебат. правилам отбора.

Изучение колебат. M. с. позволяет установить гар-монич. частоты колебаний, константы ангармонизма. По колебат. спектрам проводится конформац. анализ

(см. Конформации молекулы), изучаются межмолекулярные взаимодействия. Колебат. спектроскопия - эфф. метод качеств. и количеств. спектрального анализа в химии, биологии, медицине.

Вращательные спектры формируются при квантовых переходах между вращат. уровнями энергии молекулы. Их наблюдают обычно в поглощении методами микроволновой спектроскопии, реже в испускании и комбинац. рассеянии. Для двухатомной и линейной мно-

гоатомной молекул вращат. спектры, обусловленные дипольными электрич. переходами (изменение вращат. квантового числа DJ = b1), состоят из линий с частотами

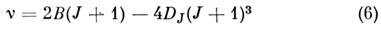
(R -ветвь; В - вращательная, D_J - центробежная постоянные, D_J << B). Вращат. спектр состоит из почти эквидистантных линий, интервал между к-рыми примерно равен 25. Вращат. спектр молекул типа симметричного волчка также прост, в соответствии с правилами отбора для таких молекул DJ = 0, b1, DK == 0, он состоит из линий с частотами

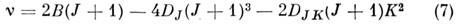
(R -ветвь). В отличие от спектров линейных молекул каждая J -линия в этом случае имеет т. н. K -структуру, соответствующую последнему члену в (7). Напр., для NH₃ D_JK =-45 МГц и с высокочастотной стороны каждой J -линии наблюдаются K -линии, отстоящие от линии с K=0на 90(J + 1)K² МГц. Правило отбора DK = Онарушается при учёте колебательно-вращат. взаимодействия, ангармонизма и нежёсткости молекулы. Вращат. спектры молекул типа асимметричного волчка более сложны, т. к. изменения чисел К _а, K_c при квантовых переходах не ограничены правилами отбора. В отличие от молекул типа симметричного волчка, у к-рых единств. компонента дипольного момента направлена по оси симметрии, у молекул типа асимметричного волчка все 3 компоненты дипольного момента могут быть отличными от нуля. Переходы, осуществляемые при взаимодействии d_a, d_b, d_c по гл. осям инерции а, b, с с электрич. вектором поля излучения, наз. переходами типа "a", "b", " с" соответственно. Эти переходы удовлетворяют след. правилам отбора по числам К _а, К _с (при условии К _а = К _с= J или J + 1): для переходов типа " а" DK _а = 0, b 2, b 4, ...; D К _c =b1, b3, b5, ...; для переходов типа " с" DK_a = b1, b3, b5, ...; D К _c =0, b2, b4,...; для переходов типа "b" DK_a = = b1, b3, ...; DK_c = b1, b3, ..., а также общим для всех переходов правилам DJ =0, b1. Эти правила отбора получаются только для жёсткого асимметричного волчка в результате применения D₂ -симметрии; для реальной нежёсткой молекулы они нарушаются. Для классификации вращат. переходов и соответствующих вращат. спектральных линий используются два способа. В первом указываются значения J, К _а, К _с обоих уровней, причём значения этих чисел для ниж. уровня всегда записываются справа. Напр., 1₁₀ - 1₁₁ означает, что J' =1, К' _а = 1, K'_c=0для верхнего и J " =1, К " _а = 1, К " _с=1 для ниж. уровня. Этот способ обозначений обычно используется для молекул типа асимметричных волчков. Для молекул типа асимметричного волчка переходы с DJ = -1, 0, +1 обозначаются лат. буквами P, Q, R соответственно, а значения J и K указываются в скобках, напр. вращат. переход P(2,1) (в комбинац. рассеянии разрешены также переходы с DJ = -2 и +2, к-рые обозначаются буквами О и S). При DK >0 значение DK указывают (индексом слева вверху) буквами о, р, q, r, s для DK = = -2, -1, 0, +1, +2 соответственно.

Во вращат. спектрах обычно наблюдаются сотни и даже тысячи линий, из частот к-рых с высокой точностью (до 1 КГц) определяются величины вращат. и центробежных констант молекул, к-рые используются при построении потенциальных поверхностей молекул. В случае нежёстких молекул, имеющих неск. равновесных конфигураций, наблюдаются туннельные расщепления вращат. линий, по к-рым определяются высота и форма барьеров на потенц. поверхности.

Колебательная структура электронных спектров. Поверхности потенц. энергии и соответствующие им системы колебат. уровней разл. электронных состояний могут существенно отличаться друг от друга, поэтому колебат. структура электронных переходов подчиняется довольно сложным правилам отбора и электронно-колебат. спектр сильно отличается от чисто колебательного. Тем не менее осн. особенности колебат. структуры поддаются не только качеств., но и количествю анализу. Теоретич. основой этого анализа является Франка - Кондона принцип, позволяющий предсказывать распределение интенсивностей полос колебат. структуры.

Рассмотрим переход между двумя электронными состояниями е' и е " двухатомной молекулы, потенц. ф-ции V(h )к-рых смещены друг относительно друга (рис. 3).

Рис. 3. Схема электронных ( е' и е " )и колебательных уровней энергии двухатомной молекулы и образо вание электронно-колебательных полос (R "_e , R'_e )в соответствии с принципом Франка - Конда.

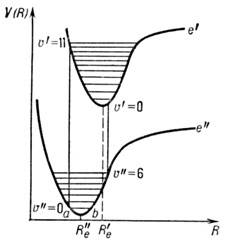
Согласно принципу Франка - Кондона, при колебат. движении атомные ядра замедляются около поворотных точек (точки а и b на кривой е "), а между поворотными точками движутся значительно быстрее. Электронный переход происходит столь быстро, что за время перехода ядра остаются в тех же поворотных точках, и поэтому наиб. вероятный путь перехода должен быть вертикальным, при этом колебат. квантовое число может изменяться, вообще говоря, на любую величину.

Электронно-колебат. система полос двухатомной молекулы состоит из прогрессий и секвенций. Если все молекулы находятся в осн. электронно-колебат. состоянии ( е " =0, u " =0), то в спектре поглощения могут наблюдаться переходы из этого состояния на все возбуждённые состояния e'u ". Совокупность этих полос наз. (u "= 0)-прогрессией (рис. 4, а, б). Аналогично переходы из состояния с u " -1 на все верх. состояния образуют (u " = 1)-прогрессию и т. д. В то же время переходы из верх. состояния e'u " на все ниж. состояния (испускание) наз. u "-прогрессиями. В гармонич. приближении для обоих состояний эти прогрессии состоят из равноотстоящих полос с частотами v₀ + w'u' (для u'-прогрессии) и v₀ - w "u " (для u "-прогрессии). Если частоты колебания w в верх, (w') и ниж. (w ") состояниях отличаются не сильно, то переходы с одинаковым значением Du =u' -u " дают близкорасположенные полосы, к-рые составляют секвенцию (рис. 4, в).

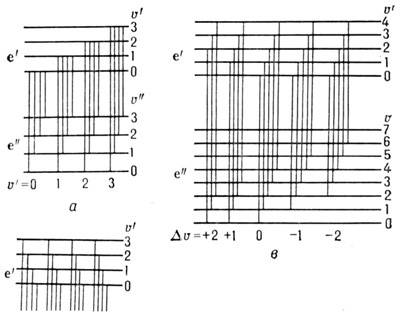
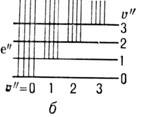
Рис. 4. Электронно-колебательные переходы, при которых образуются прогрессии ( а, б )и секвенции ( в )электронных полос.

Обычно частоты (или волновые числа) электронно-колебат. полос заносят в таблицу Деландра, к-рая строится таким образом: строки нумеруют значениями u', а столбцы - значениями u "; полосы по строке образуют u'-прогрессию, а полосы по столбцу - u "-npo-грессию. Если объединить клетки этой таблицы, содержащие наиб. интенсивные полосы кривой, то получается нек-рая парабола, симметричная относительно гл. диагонали таблицы; она наз. параболой Кондона. Чем шире парабола Кондона, тем больше отличаются друг от друга потенц. ф-ции верх. и ниж. электронных состояний.

В случае многоатомных молекул при электронном переходе одновременно изменяются квантовые числа неск. колебаний. Поэтому полосы относят к многомерным прогрессиям и секвенциям, т. к. теперь для каждого колебания возможны серии прогрессий, соответствующие разл. значениям квантовых чисел остальных колебаний.

В случае симметричных многоатомных молекул принцип Франка - Кондона ограничивает возможные переходы между колебат. уровнями энергии верх. и ниж. электронных состояний. Согласно этому принципу, не только электронный переход е' - е " должен быть разрешённым, но и т. н. фактор Франка - Кондона должен быть инвариантным относительно всех операций группы симметрии молекулы, т. е. колебат. уровни u' и u " должны относиться к одному и тому же типу симметрии. В частности, если все молекулы находятся в осн. полносимметричном вибронном состоянии, то в спектре поглощения должны наблюдаться только прогрессии полос полносимметричных колебаний, а полосы всех остальных колебаний будут запрещёнными. Для антисимметричных колебаний u_k типа A₂, B₁, А " и т. д. уровни с чётным u_k. полносимметричны, а уровни с нечётным u_k. антисимметричны. Поэтому если переход осуществляется с нек-рого уровня такого колебания, то будут разрешены только полосы секвенций с чётным Du_k (Du_k =0, b2, b4, ...).

Эти правила, справедливые только в приближении Франка - Кондона, нарушаются, и многие из запрещённых переходов можно наблюдать. Гл. причина нарушения принципа Франка - Кондона - электронно-колебат. взаимодействия, в результате к-рых приближение Борна - Оппенгеймера становится неприменимым. Кроме того, электронный дипольный момент перехода в этом случае зависит от нормальных координат. Эти обстоятельства приводят к тому, что правило отбора по типам симметрии вибронных уровней становится менее жёстким, а именно: дипольный переход между вибронными состояниями типов симметрии Г ' _еu и Г " _еu. разрешён, если прямое произведение 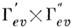содержит тип симметрии по крайней мере одной из компонент электрич. дипольного момента:

Это правило можно переформулировать: произведение волновых ф-ций нач. и конечного состояний y*_u' y_{u "} может быть неполносимметричным по отношению к тем операциям симметрии, относительно к-рых неполно-симметрично произведение y_e'*, d y_{e "}. Др. словами, запрещённый электронный или вибронный переход может стать активным, если типы симметрии y*_u' y_{u "} и y*_e' d.y _{е "} совпадают.

В электронных спектрах молекул часто наблюдаются запрещённые электронно-колебат. полосы. Напр., электронный переход B_2u - A_1g в молекуле бензола (точечная группа симметрии D_6h), запрещённый по чисто электронному правилу отбора 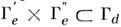, может происходить в соответствии с более точным правилом (8), если возбуждены колебания типов b_1g и e_2g, т. к. y*_e' d_zy _{е "} и y*_e' d_x,yy _{е "} относятся к типам симметрии B_1g и E_2g соответственно. Действительно, в спектре поглощения бензола наблюдается довольно сильная система полос ок. 2600 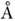с колебат. структурой, характерной для перехода B_2u - A_1g.

Вращательная структура колебательных спектров. В газовой фазе при комнатной темп-ре вращат. уровни энергии молекул заселены в соответствии с Больцмана распределением. Поэтому изменение колебат. энергии сопровождается изменением вращат. энергии. Полосы поглощения двухатомных молекул состоят из двух ветвей - R и P, соответствующих переходам с DJ = +1, DJ = - 1; Q -ветвь (DJ = 0) запрещена.

Колебат. переходы высокосимметричных молекул часто запрещены по чисто колебат. правилам отбора, но их вращат. структура разрешается вследствие эффектов колебательно-вращат. взаимодействия. Напр., в ИК-спектре поглощения метана (CH₄) из четырёх осн. полос v₁(A₁), v₂(E), v₃ и v₄(F₂) в соответствии с колебат. правилами отбора разрешены только полосы v₃ и v₄. Кориолисово взаимодействие колебания v₂ с колебаниями v₃ и v₄ приводит к активизации полосы v₂, а эффекты колебательно-вращат. взаимодействия более высокого порядка активизируют и полосу v₁, хотя чисто колебат. полосы v₁ и v₂ (J = 0) остаются запрещёнными.

Вращат. структуру колебат. полос обычно исследуют методами Фурье спектроскопии, лазерной спектроскопии, двойного ИК - MB-резонанса и др.; эти методы обеспечивают спектральное разрешение ~10^-3 см ^-1 и лучше и позволяют полностью (для лёгких молекул) или частично разрешить структуру полос. Каждая полоса наблюдается в виде сотен и даже тысяч вращат. линий. Существуют эфф. теоретич. методы для моделирования такого большого массива линий. Из частот переходов определяются величины молекулярных параметров, к-рые затем используются при построении потенц. поверхности и при расчёте частот линий в др. участках спектра.

Интенсивность отд. линий полосы и интегральная интенсивность всей полосы несут информацию о строении молекул и используются в молекулярном спектральном анализе. Относит. интенсивность линий используется обычно для идентификации линий. Интегральная интенсивность осн. полосы зависит гл. обр. от первой производной дипольного момента молекулы по данной нормальной координате. Интегральные интенсивности обертонов и составных полос зависят от более высоких производных дипольного момента по нормальным координатам и от коэф. энгармонизма. Кроме того, интенсивности отд. линий вследствие эффектов колебательно-вращат. взаимодействия зависят от определ. комбинаций дипольного момента и его производных. Поэтому измеряемые величины интенсивности линий и полос дают ценную информацию о функции дипольного момента.

Помимо дипольных переходов иногда удаётся наблюдать также переходы, обусловленные изменением квад-рупольного момента молекулы. Так, дипольные колебательно-вращат. спектры гомоядерных двухатомных молекул строго запрещены, но они имеют квадруполь-ный момент, при изменении к-рого возникают квадру-польные спектры. Такие спектры наблюдались для молекул H₂, D₂, O₂ и др.

Вращательная структура электронных спектров. Согласно принципу Франка - Кондона, при разрешённом электронном переходе тип симметрии колебат. уровня энергии не изменяется, вращат. структура виб-ронной полосы определяется гл. обр. типом электронного перехода. В частности, вращат. структура электронного перехода ¹S - ¹S двухатомной или линейной многоатомной молекулы состоит, как и в случае чисто колебат. спектра, из P- и R -ветвей, соответствующих вращат. переходам с DJ = -1 и +1 соответственно. В случае переходов ²S -²S , ³S - ³S и т. д. J заменяется на N. Если при этом спин-орбитальное взаимодействие невелико, а дублетное, триплетное и т. д. расщепления отсутствуют, то вращат. структура этих переходов будет такая же, как и перехода ¹S - ¹S. Все эти переходы связаны с проекцией электрич. дипольного момента на ось z и не имеют Q -ветви, т. к. К =L = 0. Переходы же с изменением L (П - S, D - П и т. д.) связаны с проекциями d_x и d_y( | переходы) и имеют интенсивные Q -ветви. Эффекты L-удвое-ния, спинового расщепления и др. проявляются в спектре и приводят к расщеплению P-, Q- и R -ветвей на под-ветви, причём картина расщепления зависит от того, какие взаимодействия преобладают или к какому случаю Хунда (см. Молекула )относятся рассматриваемые состояния. Напр., если ² П-состояние относится к случаю "6", то в полосе перехода ² П - ² П наблюдается простое удвоение P-, Q-, R -ветвей, а если состояние ² П относится к случаю " а", то эта полоса состоит из двух подполос, ²P_1/2- ²S и ² П _3/2 - ²S, каждая из к-рых состоит из трёх ветвей.

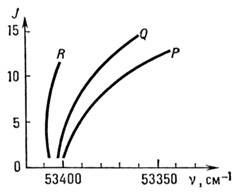
T. к. величины молекулярных констант (B, D_J и т. д.) в разл. электронных состояниях могут сильно отличаться друг от друга, структура P-, Q-, R -ветвей электронных полос может сильно отличаться от структуры этих ветвей в чисто колебат. полосах. Именно этим обусловлена более сильная сходимость линий и образование кантов (резких краёв) полос в электронных спектрах, при B' < B " образуется ВЧ-кант R -вет-ви (красное оттенение полосы), а при B' > B " образуется НЧ-кант Р -ветви (фиолетовое оттенение полосы). Образование кантов лучше всего иллюстрируется диаграммой Фортра, т. е. зависимостью J от частоты перехода (рис 5), к-рая оказывается полезной для идентификации отд. линий.

Анализ вращат. структуры вибронных полос нелинейных многоатомных молекул намного сложнее. Практически для каждого типа полос нужно вводить свою модель взаимодействий. Отметим, что если данный вибронный переход запрещён в соответствии с виброн-

ным правилом (8), он может тем не менее наблюдаться за счёт электронно-вращат. взаимодействия. Кроме того, в электронных спектрах молекул часто наблюдаются также и электрич. квадрупольные и магн. ди-польные переходы.

Рис. 5. Диаграмма Фортра для полосы 020-010 электронного перехода S - П молекулы HCN; точка схождения кривых на оси v называется кантом полосы.

Лит. см. при ст. Молекула. М. P. Алиев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.