- МИНКОВСКОГО ПРОСТРАНСТВО-ВРЕМЯ
- МИНКОВСКОГО ПРОСТРАНСТВО-ВРЕМЯ
-
четырехмерное пр-во, объединяющее физ. трёхмерное пр-во и время; введено нем. учёным Г. Минковским (Н. Minkowski) в 1907—08. Точки в М. п.-в. соответствуют «событиям» спец. теории относительности (СТО; (см. ОТНОСИТЕЛЬНОСТИ ТЕОРИЯ)). Положение события в М. п.-в. задаётся четырьмя координатами — тремя пространственными и одной временной. Обычно используются координаты xl=x, х2=у, x3=z, где х. у, z — прямоугольные декартовы координаты события в нек-рой инерциальной системе отсчёта (и. с. о.) и x°=ct, где i — время события. Геом. свойства М. п.-в. определяются выражением для квадрата расстояния между двумя событиями (интервала) s2 : s2= (Dx°)2-Dx2-Dy2-Dz2, где Dx, Dy, Dz — разности координат событий, а Dt=Dx°/с — разность их моментов времени. Пр-во с таким s2 наз. псевдоевклидовым.При переходе от одной и. с. о. к другой пространств. координаты и время преобразуются друг через друга посредством Лоренца преобразований. Введение М. п.-в. позволяет представить преобразования Лоренца как преобразование координат события x1, x2, х3, х° при поворотах четырёхмерной системы координат в этом пр-ве. Величина s2 не меняется при таких поворотах.Геометрия М. п.-в. позволяет наглядно интерпретировать кпнематич. эффекты СТО (изменение длин и скорости течения времени при переходе от одной п. с. о. к другой и т. д.) и лежит в основе совр. матем. аппарата теории относительности.
Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.
- МИНКОВСКОГО ПРОСТРАНСТВО-ВРЕМЯ
-
(Минковского пространство) - четырёхмерное пространство, точки к-рого с координатами
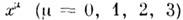 сопоставляются с событиями специальной относительности, теории. Введено в физику Г. Минковским (H. Minkowski) в 1908 с целью геом. интерпретации релятивистский теории.
сопоставляются с событиями специальной относительности, теории. Введено в физику Г. Минковским (H. Minkowski) в 1908 с целью геом. интерпретации релятивистский теории.Каждое событие характеризуется тремя пространственными координатами
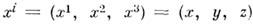 и моментом времени t, при этом удобно выбрать временную координату в виде
и моментом времени t, при этом удобно выбрать временную координату в виде 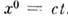 . В M. п.-в. вводится псевдоевклидова метрика, определяющая квадрат интервала -"расстояния" между бесконечно близкими событиями с координатами
. В M. п.-в. вводится псевдоевклидова метрика, определяющая квадрат интервала -"расстояния" между бесконечно близкими событиями с координатами  след, образом:
след, образом: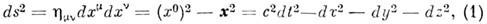
где hmv - метрич. тензор, имеющий, как видно, отличные от нуля компоненты
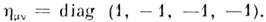 Адекватность геом. структуры M. п.-в. принципам спец. теории относительности обусловлена тем, что Лоренца преобразования, с помощью к-рых осуществляется переход от одной инорц. системы отсчёта (и. с. о.) к другой, оставляют метрич. тензор
Адекватность геом. структуры M. п.-в. принципам спец. теории относительности обусловлена тем, что Лоренца преобразования, с помощью к-рых осуществляется переход от одной инорц. системы отсчёта (и. с. о.) к другой, оставляют метрич. тензор 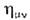 форминвариантным. Поэтому, если ур-ния физ. теории (релятивистской механики, релятивистской гидродинамики, электродинамики и др.) записаны в виде соотношений, связывающих векторы и тензоры (или спиноры), заданные в M. п.-в., то их вид будет одинаковым во всех и. с. о. Тем самым осн. принцип спец. теории относительности будет выполняться автоматически. Фактически метрика M. п.-в. инвариантна относительно более широкой группы преобразований координат-группы Пуанкаре, включающей сдвиги начала отсчёта пространств, координат и времени, повороты пространств, осей и преобразования Лоренца:
форминвариантным. Поэтому, если ур-ния физ. теории (релятивистской механики, релятивистской гидродинамики, электродинамики и др.) записаны в виде соотношений, связывающих векторы и тензоры (или спиноры), заданные в M. п.-в., то их вид будет одинаковым во всех и. с. о. Тем самым осн. принцип спец. теории относительности будет выполняться автоматически. Фактически метрика M. п.-в. инвариантна относительно более широкой группы преобразований координат-группы Пуанкаре, включающей сдвиги начала отсчёта пространств, координат и времени, повороты пространств, осей и преобразования Лоренца: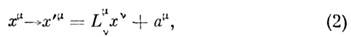
где
 а матрица
а матрица  удовлетворяет соотношениям
удовлетворяет соотношениям 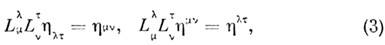
причём контравариантный метрич. тензор
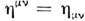 (как обычно, по повторяющемуся индексу производится суммирование).
(как обычно, по повторяющемуся индексу производится суммирование).Объединение пространства и времени в единое четырёхмерное многообразие отражает факт неабсолютности масштабов времени и пространственных расстояний, к-рыо оказываются зависящими от выбора и. с. о. Напротив, одинаковой во всех и. с. о. является скорость света с, понимаемая как универс. скорость распространения фундам. физ. взаимодействий. Промежуток времени и пространственное расстояние между двумя событиями зависят от того, в какой и. с. о. эти величины измеряются; абс. значение имеет лишь интервал между событиями, вычисляемый по ф-ле (1). Инвариантным относительно преобразований (2) (исключая отражения осей) является также элемент четырёхмерного объёма
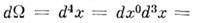
 , в то время как величины dt и элемент пространственного объёма dV по отдельности не инвариантны.
, в то время как величины dt и элемент пространственного объёма dV по отдельности не инвариантны.Метрика M. п.-в., в отличие от евклидовой, не является положительно определённой, поэтому квадрат интервала (1) может быть положительным, нулевым или отрицательным. Поскольку величина
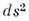 инвариантна относительно преобразований (2), это свойство не зависит от выбора и. с. о. и характеризует физически различные взаимоотношения между событиями. Если
инвариантна относительно преобразований (2), это свойство не зависит от выбора и. с. о. и характеризует физически различные взаимоотношения между событиями. Если 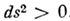 , интервал наз. времениподобным, при этом найдётся и. с. о., в к-рой эти события происходят в одной пространственной точке. Такую и. с. о. можно связать с движущейся частицей, имеющей конечную массу, тогда
, интервал наз. времениподобным, при этом найдётся и. с. о., в к-рой эти события происходят в одной пространственной точке. Такую и. с. о. можно связать с движущейся частицей, имеющей конечную массу, тогда  можно истолковать как (умноженный на с) промежуток собственного времени (т. е. измеренного по часам, движущимся вместе с частицей). Если
можно истолковать как (умноженный на с) промежуток собственного времени (т. е. измеренного по часам, движущимся вместе с частицей). Если 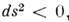 то интервал наз. пространственноподобным; в этом случае, напротив, не существует и. с. о., в к-рой события происходят в одной пространственной точке, но существует и. с. о., в к-рой эти события одновременны. Ясно, что такие события не могут быть причинно связанными друг с другом. Временная последовательность двух событий, разделённых пространственноподобным интервалом, неабсолютна; существует п. с. о., в к-рой первое событие предшествует второму, и другая и. с. о., в к-рой второе предшествует первому.
то интервал наз. пространственноподобным; в этом случае, напротив, не существует и. с. о., в к-рой события происходят в одной пространственной точке, но существует и. с. о., в к-рой эти события одновременны. Ясно, что такие события не могут быть причинно связанными друг с другом. Временная последовательность двух событий, разделённых пространственноподобным интервалом, неабсолютна; существует п. с. о., в к-рой первое событие предшествует второму, и другая и. с. о., в к-рой второе предшествует первому.Нарушение при преобразованиях Лоренца временной последовательности событий, разделённых пространственноподобным интервалом, в совокупности с принципами квантовой теории приводит к важному следствию - необходимости существования античастиц. Рассмотрим два события: P1, состоящее в испускании нейтроном
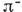 -мезона с образованием протона,
-мезона с образованием протона, 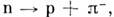 и P2, состоящее в поглощении
и P2, состоящее в поглощении 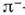 -мезона др. протоном р' с образованием нейтрона n',
-мезона др. протоном р' с образованием нейтрона n', 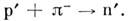 Вследствие неопределённостей соотношения имеется отличная от нуля вероятность второго события (с участием той же частицы
Вследствие неопределённостей соотношения имеется отличная от нуля вероятность второго события (с участием той же частицы 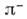 i, даже если интервал s12 между этими событиями пространственнопо-добен, при условии, что
i, даже если интервал s12 между этими событиями пространственнопо-добен, при условии, что 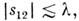 где
где 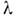 - комптонов ская длина волны
- комптонов ская длина волны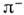 -мезона. Но тогда найдётся такая и. с. о., в к-рой поглощение
-мезона. Но тогда найдётся такая и. с. о., в к-рой поглощение 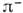 протоном наблюдалось бы до его испускания. Разрешение парадокса в квантовой теории состоит в том, что событие P2 можно понимать не как поглощение
протоном наблюдалось бы до его испускания. Разрешение парадокса в квантовой теории состоит в том, что событие P2 можно понимать не как поглощение 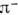 протоном, а как испускание протоном частицы той же массы, но с противоположным знаком заряда, т. е. её античастицы -
протоном, а как испускание протоном частицы той же массы, но с противоположным знаком заряда, т. е. её античастицы -
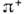 -мезона:
-мезона: 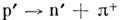 . Аналогично событие Р 1 будет состоять в поглощении p+ нейтроном с образованием протона:
. Аналогично событие Р 1 будет состоять в поглощении p+ нейтроном с образованием протона: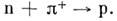
Нулевое значение интервала,
 (изотропный интервал), соответствует событиям, лежащим на мировых линиях безмассовых частиц, напр, фотонов, движущихся со скоростью с. Инвариантность равенства
(изотропный интервал), соответствует событиям, лежащим на мировых линиях безмассовых частиц, напр, фотонов, движущихся со скоростью с. Инвариантность равенства  по отношению к выбору и. с. о. и выражает собой факт постоянства скорости света во всех и. с. о.
по отношению к выбору и. с. о. и выражает собой факт постоянства скорости света во всех и. с. о.Если выбрать начало четырёхмерной системы координат в M. п.-в. в точке, отвечающей нек-рому заданному событию О, то мировые линии световых лучей, исходящих из О, будут образовывать гиперповерхность
 наз. световым конусом. Все события, лежащие внутри светового конуса (т. е. в области
наз. световым конусом. Все события, лежащие внутри светового конуса (т. е. в области 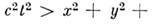
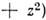 при
при  происходят в абс. будущем по отношению к О, в частности мировые линии частиц, движущихся со скоростью
происходят в абс. будущем по отношению к О, в частности мировые линии частиц, движущихся со скоростью 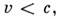 проходящие через О, в последующие моменты времени остаются внутри этой области. Аналогично события, лежащие внутри светового конуса при
проходящие через О, в последующие моменты времени остаются внутри этой области. Аналогично события, лежащие внутри светового конуса при 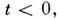 абсолютно предшествуют О. Область M. п.-в., лежащая вне светового конуса (т. е. при
абсолютно предшествуют О. Область M. п.-в., лежащая вне светового конуса (т. е. при 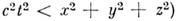 , соответствует событиям, к-рые не могут находиться в причинной связи с О, это абсолютно удалённая область. Трёхмерная гиперповерхность, проходящая через О и лежащая целиком вне светового конуса, будет пространственноподобной, в простейшем случае - это гиперплоскость, ортогональная оси времени, представляющая собой трёхмерное пространство в выбранной системе координат.
, соответствует событиям, к-рые не могут находиться в причинной связи с О, это абсолютно удалённая область. Трёхмерная гиперповерхность, проходящая через О и лежащая целиком вне светового конуса, будет пространственноподобной, в простейшем случае - это гиперплоскость, ортогональная оси времени, представляющая собой трёхмерное пространство в выбранной системе координат.Векторы в M. п.-в. (4-векторы) при преобразованиях координат из группы Пуанкаре преобразуются по ф-ле

а поднятие и опускание индексов осуществляется с помощью метрич. тензора
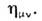 Примерами 4-векторов могут служить 4-скорость частицы ненулевой массы,
Примерами 4-векторов могут служить 4-скорость частицы ненулевой массы, 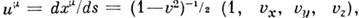 4-потенциал эл.-магн. поля
4-потенциал эл.-магн. поля 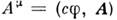 , где f - скалярный, А- векторный потенциалы. Аналогично вводятся тензоры более высокого ранга, как многоиндексные величины, испытывающие преобразования (5) по каждому из индексов, напр, тензор эл.-магн. поля
, где f - скалярный, А- векторный потенциалы. Аналогично вводятся тензоры более высокого ранга, как многоиндексные величины, испытывающие преобразования (5) по каждому из индексов, напр, тензор эл.-магн. поля 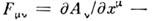
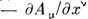
Преобразования координат более общего вида, чем (2), уже не будут оставлять метрич. тензор форминва-риантным, это произойдёт, напр., при переходе к не-инерц. системе отсчёта. Разумеется, введение в M. п.-в. криволинейных координат не изменяет плоского характера геометрии M. п.-в. (в противоположность искривлённому пространству-времени при наличии гравитац. полей). Это выражается в равенстве нулю во всех точках пространства-времени кривизны тензора
 для метрики
для метрики 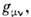 получаемой из
получаемой из 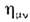 произвольным преобразованием координат. Напротив, при наличии гравитац. поля
произвольным преобразованием координат. Напротив, при наличии гравитац. поля  нельзя обратить в нуль сразу во всём пространстве-времени, однако в малой пространственно-временной области можно выбрать координаты так, что метрич. тензор
нельзя обратить в нуль сразу во всём пространстве-времени, однако в малой пространственно-временной области можно выбрать координаты так, что метрич. тензор 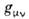 будет отличаться от метрики Минковского лишь на величины второго порядка малости (переход в свободно падающую систему отсчёта). T. о., искривлённое пространство-время общей теории относительности в достаточно малых областях по-прежнему описывается геометрией M. п.-в.
будет отличаться от метрики Минковского лишь на величины второго порядка малости (переход в свободно падающую систему отсчёта). T. о., искривлённое пространство-время общей теории относительности в достаточно малых областях по-прежнему описывается геометрией M. п.-в.Лит.: Ландау Л. Д., JIифшиц E. M., Теория поля, 7 изд., M., 1988; Минковский Г., Пространство и время, в кн.: Принцип относительности, M., 1973; Mизнер Ч., Торн К., Уилер Дж., Гравитация, пер. с англ., т. 1, M., 1977. Д. В. Гальцов.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
.
