МАГНИТОМЕХАНИЧЕСКОЕ ОТНОШЕНИЕ

МАГНИТОМЕХАНИЧЕСКОЕ ОТНОШЕНИЕ
МАГНИТОМЕХАНИЧЕСКОЕ ОТНОШЕНИЕ

       
(гиромагнитное отношение), отношение магнитного момента элем. ч-ц (и состоящих из них систем — атомов, молекул, ат. ядер и т. д.) к их моменту кол-ва движения (механич. моменту). Для каждой элем. ч-цы, обладающей отличным от нуля механич. моментом — спином, М. о. имеет определ. значение. Для разл. состояний ат. системы значения М. о. определяются по ф-ле: g=gg0, где g0 — единица М. о., g — Ланде множитель. В этом случае за единицу М. о. принимают его величину для орбит. движения эл-на в атоме: —е/2mес, где е — заряд эл-на, me — масса эл-на. Для ядер за единицу М. о. принимают аналогичную величину для протона: е!2mрС (mр — масса протона).
Величина М. о. определяет действие магн. поля на систему, обладающую магн. моментом. Согласно классич. теории, магн. момент во внеш. магн. поле напряжённостью Н совершает прецессию — равномерно вращается вокруг направления Н, сохраняя определ. угол наклона, с угл. скоростью w=-gН. В частном случае, когда магн. момент обусловлен орбит. движением эл-нов, имеет место Лармора прецессия. Согласно квант. теории, масштаб магн. расщепления уровней энергии в магн. поле (см. ЗЕЕМАНА ЭФФЕКТ) определяется М. о., он равен: gћН= gg0nћH.

Физический энциклопедический словарь. — М.: Советская энциклопедия. . 1983.

МАГНИТОМЕХАНИЧЕСКОЕ ОТНОШЕНИЕ

(гиромагнитное отношение) - отношение магн. момента 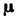2573-1.jpg частицы (электрона, протона, атома, атомного ядра и т. д.) к её механич. моменту К. Для атомов 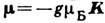2573-2.jpg, где g - Ланде множитель (фактор Ланде, или g- фактор), 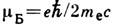2573-3.jpg- магнетон Бора ( е, m е - заряд и масса электрона). В зависимости от моментов (орбитального L, спинового S )различают орбитальный gL и спиновый gs факторы Ланде.

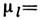
Для электрона орбитальный магн. момент 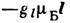2573-4.jpg2573-5.jpg (l - его орбитальный момент) и gl=1; спиновый магн. момент 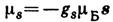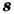2573-6.jpg (2573-7.jpg- спин электрона), эксперим. значение gs=2,0023293044. Аномалия магн. момента 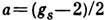2573-8.jpg связана с эффектами квантовой электродинамики.

Для атома с полным электронным моментом J магн. момент 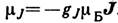2573-9.jpg . При LS- связи(см. Связь векторная) gJ для полных моментов равен:

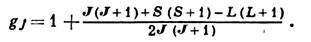
2573-10.jpg

Для многоэлектронных атомов расчёт gJ представляет собой трудоёмкую задачу.

Магн. моменты атомных ядер выражают в ядерных магнетонах 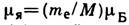2573-11.jpg , где М - масса протона. Для протона (р) и нейтрона (n) магн. момент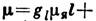 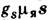2573-12.jpg2573-13.jpg, множитель Ланде для протона gl (р)=1, а для нейтрона 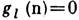2573-14.jpg; эксперим. данные gs -фактора составляют: gs(p) = 5,58569227, gs(n) = -3,82608368.

Для ядер обычно приводятся не g -факторы, а величины магн. момента ядра (см. Ядерный спин).

Лит.: Вонсовский С. В., Магнетизм микрочастиц, М., 1973; Proceedings of the second International conference on fundamental constants, Gaithersburg. MD, June 8-12, 1981 (NBS Special Publication № 617, 1984). В. П. Шевелъко.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. . 1988.


.

Игры ⚽ Нужно решить контрольную?

Полезное


Смотреть что такое "МАГНИТОМЕХАНИЧЕСКОЕ ОТНОШЕНИЕ" в других словарях:

  • МАГНИТОМЕХАНИЧЕСКОЕ ОТНОШЕНИЕ — (гиромагнитное отношение) отношение магнитного момента элементарных частиц (и их систем) к их механическому моменту. Определяет действие магнитного поля на такие частицы (Лармора прецессия, Зеемана эффект) …   Большой Энциклопедический словарь

  • магнитомеханическое отношение — (гиромагнитное отношение), отношение магнитного момента элементарных частиц (и их систем) к их механическому моменту. Определяет действие магнитного поля на такие частицы (Лармора прецессия, Зеемана эффект). * * * МАГНИТОМЕХАНИЧЕСКОЕ ОТНОШЕНИЕ… …   Энциклопедический словарь

  • магнитомеханическое отношение — magnetomechaninis santykis statusas T sritis fizika atitikmenys: angl. magnetomechanical factor; magnetomechanical ratio vok. magnetomechanischer Faktor, m; magnetomechanisches Verhältnis, n rus. магнитомеханическое отношение, n pranc. facteur… …   Fizikos terminų žodynas

  • Магнитомеханическое отношение — Гиромагнитное отношение (магнитомеханическое отношение) отношение дипольного магнитного момента элементарной частицы (или системы элементарных частиц) к её механическому моменту. В системе СИ единицей измерения гиромагнитного отношения является… …   Википедия

  • Магнитомеханическое отношение —         гиромагнитное отношение, отношение магнитного момента (См. Магнитный момент) элементарных частиц (и состоящих из них систем атомов, молекул, атомных ядер и т.д.) к их моменту количества движения (механическому моменту). Для каждой… …   Большая советская энциклопедия

  • МАГНИТОМЕХАНИЧЕСКОЕ ОТНОШЕНИЕ — (гиромагнитное отношение), отношение магн. момента элементарных частиц (и их систем) к их мсханич. моменту. Определяет действие магн. поля на такие частицы (Лармора прецессия, Зеемана эффект) …   Естествознание. Энциклопедический словарь

  • Гиромагнитное отношение —         отношение магнитного момента атомных частиц (электронов, протонов, нейтронов, атомных ядер и т.д.) к их моменту количества движения. Подробнее см. Магнитомеханическое отношение …   Большая советская энциклопедия

  • гиромагнитное отношение — то же, что магнитомеханическое отношение. * * * ГИРОМАГНИТНОЕ ОТНОШЕНИЕ ГИРОМАГНИТНОЕ ОТНОШЕНИЕ, то же, что магнитомеханическое отношение (см. МАГНИТОМЕХАНИЧЕСКОЕ ОТНОШЕНИЕ) …   Энциклопедический словарь

  • Гиромагнитное отношение — (магнитомеханическое отношение) отношение дипольного магнитного момента элементарной частицы (или системы элементарных частиц) к её механическому моменту. В системе СИ единицей измерения гиромагнитного отношения является с·А·кг−1 = с−1·Тл−1.… …   Википедия

  • ГИРОМАГНИТНОЕ ОТНОШЕНИЕ — то же, что магнитомеханическое отношение …   Большой Энциклопедический словарь


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»