КИНЕТИЧЕСКОЕ УРАВНЕНИЕ БОЛЬЦМАНА

КИНЕТИЧЕСКОЕ УРАВНЕНИЕ БОЛЬЦМАНА
КИНЕТИЧЕСКОЕ УРАВНЕНИЕ БОЛЬЦМАНА

       
интегродифференциальное уравнение, к-рому удовлетворяют неравновесные одночастичные функции распределения систем из большого числа ч-ц, напр. ф-ция распределения f(v, r, t) молекул газа по скоростям v и координатам r, ф-ции распределения эл-нов в металле, фононов в кристалле и т. п. (см. КИНЕТИКА ФИЗИЧЕСКАЯ). К. у. Б.— осн. ур-ние микроскопич. теории неравновесных процессов, физ. кинетики, в частности кинетической теории газов. К. у. Б. в узком смысле наз. кинетич. ур-ние для газов малой плотности. Различные обобщения К. у. Б., напр. для квазичастиц в кристаллах, для эл-нов в металле, также наз. К. у. Б., просто кинетич. ур-ниями или ур-ниями переноса.
К. у. Б. представляет собой ур-ние баланса числа ч-ц (точнее, точек, изображающих состояние ч-ц) в элементе фазового объема dvdr (dv=dvxdvydvz, dr=dxdydz) и выражает тот факт, что изменение ф-ции распределения ч-ц f(v, r, t) со временем t происходит вследствие движения ч-ц под действием внеш. сил и столкновений между ними. Для газа, состоящего из ч-ц одного сорта, К. у. Б. имеет вид:
КИНЕТИЧЕСКОЕ УРАВНЕНИЕ БОЛЬЦМАНА1
где f(v, r, t) dvdr — ср. число ч-ц в элементе фазового объёма dvdr около точки (v, r); F=F(r, t) — сила, действующая на ч-цу;(дf/дt)ст — изменение ф-ции распределения вследствие столкновении; дf/дt — изменение плотности числа ч-ц около точки (v, r) в момент времени t за ед. времени. Второй и третий члены ур-ния (1) характеризуют соотв. изменение ф-ции распределения в результате перемещения ч-ц в пр-ве и действия внеш. сил. Её изменение, обусловленное столкновениями ч-ц, связано с уходом ч-ц из элемента фазового объёма при т. н. прямых столкновениях и пополнением объёма ч-цами, испытавшими «обратные» столкновения. Если рассчитывать столкновения по законам классич. механики и считать, что нет корреляции между динамич. состояниями сталкивающихся молекул, то в К. у. Б. (1)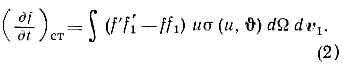
КИНЕТИЧЕСКОЕ УРАВНЕНИЕ БОЛЬЦМАНА2
Здесь f(v, r, t) и f1(v1, r, t) — ф-ции распределения до столкновения, f' (v', r, t) и f'1(v'1, r, t) — после столкновения, v и v1— скорости ч-ц до столкновения, v', v'1— скорости тех же ч-ц после столкновения, u=?v-v1? — модуль относит. скорости сталкивающихся ч-ц, q — угол между относит. скоростью v-v1 сталкивающихся молекул и линией, соединяющей их центры, s(u, q) dW — дифференциальное эфф. сечение рассеяния ч-ц на телесный угол dW в лаб. системе, зависящее от закона вз-ствия молекул. Для модели молекул в виде упругих жёстких сфер, имеющих радиус R, s=4R2cosq. К. у. Б. (1) было выведено австр. физиком Л. Больцманом (L. Boltzmann) в 1872.
К. у. Б. учитывает только парные столкновения между молекулами; оно справедливо при условии, что длина свободного пробега молекул значительно больше линейных размеров области, в к-рой происходит столкновение (для газа из упругих ч-ц сферич. формы это область порядка диаметра ч-ц). Поэтому К. у. Б. применимо для не слишком плотных газов. Иначе будет несправедливо осн. предположение об отсутствии корреляции между состояниями сталкивающихся молекул (гипотеза мол. хаоса). Если система находится в равновесии статистическом, то интеграл столкновений (2) обращается в нуль и решением К. у. Б. будет Максвелла распределение. Найденное для соответствующих условий решение К. у. Б. позволяет вычислить кинетические коэффициенты и получить макроскопич. ур-ния для разл. процессов переноса (вязкости, диффузии, теплопроводности и др.). Для квант. газов значения эфф. сечений рассчитываются на основе квант. механики (с учётом неразличимости одинаковых ч-ц и того факта, что вероятность столкновения определяется не только хар-ром ф-ций распределения ч-ц до столкновения, но и хар-ром этих ф-ций после столкновения). Для фермионов учёт этих факторов приводит к уменьшению вероятности столкновений, а для бозонов— к увеличению. Интеграл столкновений в этом случае имеет более сложный вид (содержит ff1(1±f'1) (1± f'1) вместо ff1, где верхний знак относится К Ферми — Дирака статистике, а нижний — к Возе — Эйнштейна статистике). Ферми—Дирака распределение и Бозе — Эйнштейна распределение явл. решениями соответствующих квант. К. у. Б. для случая статистич. равновесия.

Физический энциклопедический словарь. — М.: Советская энциклопедия. . 1983.


.

Игры ⚽ Нужна курсовая?

Полезное


Смотреть что такое "КИНЕТИЧЕСКОЕ УРАВНЕНИЕ БОЛЬЦМАНА" в других словарях:

  • КИНЕТИЧЕСКОЕ УРАВНЕНИЕ БОЛЬЦМАНА — интегродифференц. ур ние, к рому удовлетворяют неравновесные одночастичные функции распределения системы из большого числа частиц, напр, ф ция распределения молекул газа по скоростям и координатам r, ф ции распределения электронов в металле,… …   Физическая энциклопедия

  • Кинетическое уравнение Больцмана — Уравнение Больцмана (кинетическое уравнение Больцмана)  уравнение, названное по имени Людвига Больцмана, который его впервые рассмотрел, и описывающее статистическое распределение частиц в газе или жидкости. Является одним из самых важных… …   Википедия

  • Кинетическое уравнение Больцмана —         уравнение для функции распределения f (ν, r, t) молекул газа по скоростям ν и координатам r (в зависимости от времени t), описывающее неравновесные процессы в газах малой плотности. Функция f определяет среднее число частиц со скоростями… …   Большая советская энциклопедия

  • КИНЕТИЧЕСКОЕ УРАВНЕНИЕ — уравнение неравновесной статистпч. физики, используемое в теории газов, аэродинамике, физике плазмы, теории прохождения частиц через вещество, теории переноса излучения. Решение К. у. определяет функцию распределения дпнамич. состояний одной… …   Математическая энциклопедия

  • КИНЕТИЧЕСКОЕ УРАВНЕНИЕ ОСНОВНОЕ — ур ние для вероятности распределения квантовой системы по квантовым состояниям. Установлено В. Паули (W. Pauli) в 1928. К. у. о. является квантовым кинетич. ур нием, иногда его наз. управляющим ур нием (master equation) или ур нием Паули, из него …   Физическая энциклопедия

  • КИНЕТИЧЕСКОЕ УРАВНЕНИЕ — 1) в статистиче ской физике уравнение для одночастичной функции распределения системы мн. частиц (дающей ср. число частиц с определ. значениями импульсов и координат), описывающее эволюцию системы во времени. К. у. для газа было впервые… …   Естествознание. Энциклопедический словарь

  • Основное кинетическое уравнение — феноменологическое уравнение, описывающее эволюцию системы во времени. Установлено В. Паули в 1928 году. Название «основное уравнение» перевод термина англ. Master equation. Называется также производящее или управляющее уравнение. Для… …   Википедия

  • Уравнение —         в математике, аналитическая запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны. Аргументы, от которых зависят эти функции, называются обычно неизвестными, а значения неизвестных, при которых… …   Большая советская энциклопедия

  • Уравнение Смолуховского — Не следует путать с Соотношение Эйнштейна Смолуховского. Уравнение Смолуховского  кинетическое уравнение, описывающее эволюцию функции распределения координат и скороостей частиц при одномерном броуновском движении. где   функция… …   Википедия

  • Больцмана уравнение — кинетическое (по имени австрийского физика Л. Больцмана (L. Boltzmann); 1844 1906) интегро дифференциальное уравнение для функции распределения f (v, г. t) молекул газа по скорости v и координатам радиус вектору r (в зависимости от времени t.… …   Энциклопедия техники


Поделиться ссылкой на выделенное

Прямая ссылка:
… Нажмите правой клавишей мыши и выберите «Копировать ссылку»