КИНЕМАТИКА

КИНЕМАТИКА

       

(от греч. kinema, род. п. kinematos — движение), раздел механики, посвящённый изучению геом. св-в движений тел, без учёта их масс и действующих на них сил. Методы и зависимости, устанавливаемые в К., используются при кинематич. исследованиях движений, в частности при расчётах передач движений в разл. механизмах, машинах и др., а также при решении задач динамики. В зависимости от св-в изучаемого объекта К. разделяют на К. точки, К. тв. тела и К. непрерывной изменяемой среды (деформируемого тв. тела, жидкости, газа).

Движение любого объекта в К. изучают по отношению к нек-рому телу (тело отсчёта), с к-рым связывают т. н. систему отсчёта (оси х, у, г на рис. 1), позволяющую определять положение движущегося объекта в разные моменты времени относительно тела отсчёта.

Выбор системы отсчёта в К. произволен и зависит от целей исследования. Напр., при изучении движения колеса вагона по отношению к рельсу систему отсчёта связывают с Землёй, а при изучении движения того же колеса по отношению к кузову вагона — с кузовом и т. д. Движение рассматриваемого объекта считается заданным (известным), если известны ур-ния (или графики, таблицы), позволяющие определить положение этого объекта по отношению к системе отсчёта в любой момент времени.

Осн. задача К.— установление (при помощи тех или иных матем. методов) способов задания движения точек или тел и определение соответствующих кинематич. хар-к этих движений (траектории, скорости и ускорения движущихся точек, угл. скорости и угл. ускорения вращающихся тел и др.).

Движение точки может быть задано одним из трёх способов: векторным, координатным или естественным. При векторном способе положение точки по отношению к системе отсчёта определяется её радиусом-вектором r, проведённым от начала отсчёта до движущейся точки, а закон движения даётся векторным ур-нием: r=r(t). Траекторией точки явл. годограф вектора r. При координатном способе положение точки относительно системы отсчёта определяется к.-л. тремя координатами, напр. прямоугольными декартовыми х, у, z, а закон движения задаётся тремя ур-ниями: x=f1(t), y=f2(t), z=f3(t). Исключив из этих ур-ний время t, можно найти траекторию точки. Естественный (или траекториый) способ применяется обычно, когда известна траектория точки по отношению к выбранной системе отсчёта. Положение точки определяется расстоянием s=О1М от выбранного на траектории начала отсчёта O1, измеренным вдоль траектории и взятым с соответствующим знаком (рис. 1), а закон движения даётся ур-нием s=f(t), выражающим зависимость s от времени t. Зависимость s от t может быть также задана графиком движения, на к-ром в выбранном масштабе вдоль оси t отложено время, а вдоль s — расстояние (рис. 2), или таблицей, где в одном столбце даются значения t, а в другом — соответствующие им значения s. Осн. кинематич. хар-ками движущейся точки явл. её скорость и ускорение.

Способы задания движения тв. тела зависят от вида его движения, а число ур-ний движения — от числа степеней свободы тела (см. СТЕПЕНЕЙ СВОБОДЫ ЧИСЛО). Простейшими явл. поступательное движение и вращательное движение тв. тела. При поступат. движении все точки тела движутся одинаково, и его движение задаётся и изучается так же, как движение одной точки. При вращат. движении вокруг неподвижной оси АВ (рис. 3) тело имеет одну степень свободы; его положение определяется углом поворота j, а закон движения задаётся ур-нием: j=f(t). Осн. кинематич. хар-ками явл. угловая скорость w и угловое ускорение e тела. Зная w и e, можно определить скорость и ускорение любой точки тела.

Более сложным явл. движение тела, имеющего одну неподвижную точку и обладающего тремя степенями свободы (напр., гироскоп). В этом случае положение тела относительно системы отсчёта определяется к.-н. тремя углами (напр., Эйлеровыми углами), а закон движения — ур-ниями, выражающими зависимость этих углов от времени. Осн. кинематич. хар-ками явл. w и e тела. Движение тела слагается из серии элем. поворотов вокруг непрерывно меняющих своё направление мгновенных осей вращения ОР, проходящих через неподвижную точку О (рис. 4).

Самый общий случай — движение свободного тв. тела, имеющего шесть степеней свободы. Положение тела определяется тремя координатами одной из его точек, наз. полюсом (в задачах динамики за полюс принимается обычно центр тяжести тела), и тремя углами, к-рые выбираются так же, как для тела с неподвижной точкой. Закон движения тела задаётся шестью ур-ниями, выражающими зависимости названных координат и углов от времени. Движение тела слагается из поступательного вместе с полюсом и вращательного вокруг этого полюса, как вокруг неподвижной точки. Такими, напр., являются: движение в воздухе артиллерийского снаряда или самолёта, совершающего фигуры высш. пилотажа, движения небесных тел. Осн. кинематич. хар-ки — скорость и ускорение поступат. части движения, равные скорости и ускорению полюса, и угл. скорость и угл. ускорение вращения тела вокруг полюса. Все названные хар-ки (как и кинематич. хар-ки для тела с неподвижной точкой) определяются по ур-ниям движения; зная эти хар-ки, можно вычислить скорость и ускорение любой точки тела. Частным случаем рассмотренного движения явл. плосконаправленное (или плоское) движение тв. тела, при к-ром все его точки движутся параллельно нек-рой плоскости. Подобное движение совершают звенья многих механизмов и машин.

В К. изучают также сложное движение точек или тел, т. е. движение, рассматриваемое одновременно по отношению к двум (или более) взаимно перемещающимся системам отсчёта. При этом одну из систем отсчёта рассматривают как основную (её условно наз. неподвижной), а перемещающуюся по отношению к ней систему отсчёта наз. подвижной; в общем случае подвижных систем отсчёта может быть несколько. При изучении сложного движения точки её движение, а также скорость и ускорение по отношению к осн. системе отсчёта наз. условно абсолютными, а по отношению к подвижной системе — относительными. Движение самой подвижной системы отсчёта и всех неизменно связанных с нею точек np-ва по отношению к осн. системе наз. п е р е н о с н ы м движением. Осн. задачи К. сложного движения заключаются в установлении зависимостей между кинематич. хар-ками абс. и относит. движений точки (или тела) и хар-ками движения подвижной системы отсчёта, т. е. переносного движения (см. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ).

Для тв. тела, когда все составные (т. е. относительные и переносные) движения явл. поступательными, абс. движение также поступательное со скоростью, равной геом. сумме скоростей составных движений. Если составные движения тела явл. вращательными вокруг осей, пересекающихся в одной точке (как, напр., у гироскопа), то результирующее движение также явл. вращательным вокруг этой точки с угл. скоростью, равной геом. сумме угл. скоростей составных движений. Если же составными движениями тела явл. и поступательные и вращательные, то результирующее движение в общем случае будет слагаться из серии мгновенных винтовых движений.

В К. сплошной среды устанавливаются способы задания движения этой среды, рассматривается общая теория деформаций и определяются т. н. ур-ния неразрывности (сплошности) среды (подробнее (см. ГИДРОМЕХАНИКА, УПРУГОСТИ ТЕОРИЯ)).

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

КИНЕМАТИКА

- раздел механики, в к-ром изучаются геом. свойства движения тел без учёта их массы и действующих на них сил. Исходными в К. являются понятия пространства и времени. В этой статье излагается К. движений, изучаемых в классич. механике; о К. движений со скоростями, близкими к скорости света, см. Релятивистская механика (о движениях микрочастиц см. Квантовая механика).

В зависимости от свойств изучаемого объекта К. можно разделить на: К. точки и твёрдого тела; К. деформируемой частицы и непрерывной деформируемой среды (упруго или пластически деформируемое тело, жидкость, газ).

Осн. задачами К. точки и твёрдого тела являются: описание (с помощью матем. ур-ний, графиков или таблиц) движений, совершаемых точками или телами по отношению к данной системе отсчёта, и определение всех кинематич. характеристик этих движений; изучение сложных (составных) движений точек или тел, т. е. движений, совершаемых по отношению к нескольким взаимно перемещающимся системам отсчёта, и определение зависимостей между характеристиками этих движений.

Положение точки или тела по отношению к данной системе отсчёта определяется к.-л. независимыми между собой параметрами (координатами) g₁, q₂, . . ., q_n, число п к-рых равно числу степеней свободы точки или тела (для точки , для твёрдого тела ). Чтобы описать движение точки или тела по отношению к данной системе отсчёта, нужно знать его положение по отношению к этой системе в любой момент времени, т. е. определить координаты q_i как ф-ции времени t. Ур-ния

определяющие т. н. закон движения точки или тела по отношению к данной системе отсчёта, наз. кинематич. ур-ниями движения. Аналогично определяется закон движения любой механич. системы точек или тел (напр., механизма). Ф-ции, входящие в ур-ния (1), должны быть однозначными (т. к. система не может занимать в данный момент времени 2 разных положения в пространстве) н дважды дифференцируемыми (что необходимо для вычисления скоростей и ускорений). Если движение задано в течение к.-н. интервала времени , то и ф-ции (1) должны быть определены для этого интервала. В зависимости от того, будут ли ф-ции (1) заданы аналитически, численно (таблицами) или графически, для решения задач К. могут применяться ана-литич., численные или графич. методы.

Рассматриваемые обычно в механике кинематич. характеристики движения выражаются через первые и вторые производные от координат q_i по времени (иногда, напр. в кинематике механизмов, используются характеристики, выражаемые и через производные более высокого порядка). Число и вид этих характеристик связаны с особенностями рассматриваемого движения.

Движение свободной точки М (рис. 1) определяется тремя ур-ниями вида (1), где q₁, q₂, q₃ - координаты точки (декартовы, цилиндрические, сферические или др.). Одновременно эти 3 ур-ния являются параметрич. ур-ниями траектории точки. Если траектория точки известна заранее, то закон движения точки можно ещё задать ур-нием s=f(t), где s=O₁M - расстояние точки от выбранного на траектории начала отсчёта O₁, измеренное вдоль траектории и взятое с соответствующим знаком. Кинематич. характеристики движения точки - её скорость и ускорение

Число ур-ний, определяющих закон движения твёрдого тела и его кинематич. характеристики, зависит от вида движения тела. Простейшими являются поступательное движение и вращательное движение твёрдого тела. При поступат. движении все точки тела движутся одинаково и для задания движения тела достаточно задать движение к.-н. одной его точки, наз. полюсом. Следовательно, поступат. движение тела задаётся так же. как движение точки.

Рис. 1.

Рис. 2.

При вращат. движении вокруг неподвижной оси (рис. 2) тело имеет одну степень свободы и его положение определяется углом поворота . Закон этого движения даётся ур-нием . Кинематич. характеристики движения - угл. скорость и угл. ускорение тела.

Более сложным случаем вращат. движения является движение тела, имеющего одну неподвижную точку (примером такого движения может служить движение гироскопа). В этом случае тело имеет 3 степени свободы и его движение описывается тремя ур-ниями вида (1), где q₁, q₂, и q₃ могут быть, напр., Эйлера углами и . Движение тела около неподвижной точки слагается из серии элементарных поворотов вокруг мгновенных осей вращения, проходящих через эту точку. Осн. кинематич. характеристики движения - вектор мгновенной угл. скорости , направленный по мгновенной оси вращения, и вектор мгновенного угл. ускорения , направленный параллельно касательной к кривой, описываемой концом вектора

В общем случае движения свободное твёрдое тело имеет 6 степеней свободы и его движение описывается шестью ур-ниями вида (1). Параметрами q_i в этом случае могут служить координаты х _C , у _C , z_C к.-н. точки С тела, выбранной в качестве полюса, и углы Эйлера , определяющие положение тела по отношению к осям, перемещающимся поступательно вместе с полюсом. В задачах динамики в качестве полюса выбирается обычно центр масс (центр тяжести) тела.

Движение свободного твёрдого тела слагается из поступат. движения вместе с полюсом С и серии элементарных поворотов вокруг мгновенных осей вращения, проходящих через этот полюс. Примерами такого рода движения являются движения в воздухе артиллерийских снарядов, ракет, самолётов, движения небесных тел и др. Кинематич. характеристиками движения служат поступат. скорость и поступат. ускорение, равные скорости и ускорению полюса, а также мгновенная угл. скорость и мгновенное угл. ускорение движения тела вокруг полюса. Важно отметить, что от выбора полюса величины 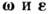не зависят и вычисляются так же, как при движении тела около неподвижной точки. Скорость и ускорение 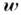любой точки М тела в этом движении слагаются геометрически из скорости (или ускорения) полюса С и скорости (ускорения), получаемых точкой М при вращении тела вокруг полюса. Кроме того, при любом движении твёрдого тела проекции скоростей и 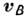к.-н. двух его точек А и В на прямую АВ равны друг другу. Частным случаем рассмотренного движения является плоскопараллельное движение твёрдого тела, при к-ром все точки тела движутся параллельно нек-рой неподвижной плоскости.

Сложным или составным движением точки (или тела) наз. движение, рассматриваемое одновременно по отношению к двум (и более) системам отсчёта, из к-рых одна условно считается неподвижной, а другая опре-дел. образом движется по отношению к первой. Движение, совершаемое при этом точкой или телом по отношению к подвижной системе отсчёта, наз. о т н о с и-т е л ь н ы м; движение самой подвижной системы отсчёта и всех неизменно связанных с ней точек по отношению к системе, принимаемой за неподвижную, является для движущейся точки (тела) переносным; наконец, движение точки (тела) по отношению к системе отсчёта, принимаемой за неподвижную, наз. абсолютным или сложным.

Абс. скорость точки, совершающей сложное движение, равна геом. сумме относительной и переносной скоростей:

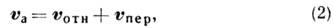
а абс. ускорение 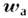равно геом. сумме трёх ускорений: относительного, переносного и поворотного, или Кори-олиса ускорения:

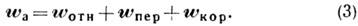
При сложном движении твёрдого тела, когда его составные движения являются поступательными, абс. движение тела также будет поступательным со скоростью, определяемой равенством (2). Если составные движения тела - вращательные вокруг двух пересекающихся или параллельных мгновенных осей вращения, причём , то результирующее движение будет также вращательным с угл. скоростью . В случае, когда 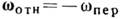, т. е. когда составными движениями тел являются мгновенные вращения вокруг двух параллельных осей с угл. скоростями, равными по модулю и противоположными по направлению (пара вращений), результирующим движением будет мгновенное поступат. движение со скоростью 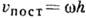(рис. 3), направленной так же, как направлен вектор момента пары сил. Если составными движениями тела являются вращение вокруг нек-рой оси и поступат. движение по направлению, параллельному этой оси, то результирующим движением тела является винтовое движение. В самом общем случае, когда тело одновременно участвует в ряде мгновенных вращат. и поступат. движений, его результирующее движение есть мгновенное винтовое.

В задачи К. деформируемой среды входит рассмотрение общей теории деформаций и определение т. н. ур-ний неразрывности, отражающих условие непрерывности среды, а также установление методов задания движения непрерывной среды и определение кинематич. характеристик этого движения (подробнее см. Упругости теория и Гидроаэромеханика).

Устанавливаемые в К. понятия и зависимости используются как вспомогательные при решении задач динамики. Кроме того, методы К. имеют самостоят. значение при расчётах передач движений в разл. механизмах, машинах и др.

Лит.: Жуковский Н. Е., Теоретическая механика, 2 изд., М.-Л., 1952; Лойцянский Л. Г., Лурье А. И., Курс теоретической механики, т. 1 - Статика и кинематика, 8 изд.,М., 1982; см. также лит. при ст. Механика.

С. М. Таре.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.