НАЙКВИСТА ФОРМУЛА

НАЙКВИСТА ФОРМУЛА

       

(теорема Найквиста), соотношение, определяющее величину тепловых флуктуаций тока или напряжения в электрич. цепи. Получено амер. физиком X. Найквистом (Н. Nyquist) в 1928. Согласно Н. ф., обусловленное тепловыми флуктуациями ср. значение квадрата напряжений на концах проводника с сопротивлением R, находящегося в состоянии теплового равновесия при абс. темп-ре Т, равно:

V2 = 4RkTDv, (1)

где Dv — полоса частот, внутри к-рой измеряются флуктуации напряжения. При низких темп-pax и достаточно высоких частотах v, когда hv?kT, вместо формулы (1) пользуются более общим выражением: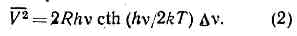

Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

НАЙКВИСТА ФОРМУЛА

- соотношение, описывающее распределение по частотам тепловых флуктуации тока или напряжения в квазистационарной пассивной электрич. цепи. Установлена X. Найквистом (H. Nyquist) в 1927, к-рый показал, что флуктуации тока в цепи можно рассматривать как следствие флуктуации случайной эдс, локализованной в цепи.

Согласно H. ф., спектральная плотность (E²)w временной корреляционной функции<E(t)E(0)>. (флуктуации) случайных эдс E(t )в произвольной квазистационарной пассивной электрич. цепи с импедансом Z(w)равна

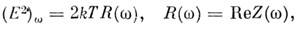
где ( Е ²)_w. связана с корреляц. ф-цией эдс соотношением

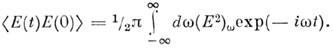
Спектральная плотность флуктуации тока

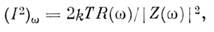
т. к. в линейной цепи Е_w =Z(w)I_w, где E_w. и I_w - фурье-компоненты E(t )и I(t). Необходимое для вывода H. ф. условие квазистационарности выполняется, если размеры электрич. цепи малы по сравнению с длиной волны l ~ c/w; тогда ток одинаков для всех участков цепи.

H. ф. справедлива для достаточно низких частот и высоких темп-р, когда w << kT и можно пренебречь квантовыми эффектами. Если это условие не выполнено, имеет место обобщённая H. ф., выведенная X. Кал-леном (H. В. Gallen) и T. Уэлтоном (Th. A. Welton) в 1951, согласно к-рой

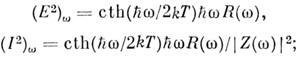
спектральные плотности (E²)_w,(I²)_w в этом случае определены по отношению к симметризованным временным корреляц. ф-циям вида (¹/₂)<E(t)E(0)+ + E(0)E(t)>. (аналогично для тока). Эти ф-лы являются частным случаем флуктуационно-диссипа-тивной теоремы, к-рая определяет связь между флук-туациями системы в равновесном состоянии и её дис-сипативными свойствами.

Из H. ф. следует, что флуктуации тока связаны с диссипацией в цепи и системы, не обладающие активным сопротивлением, не содержат источника теплового шума. H. ф. применима только к достаточно хорошим проводникам, для к-рых на данной частоте w можно пренебречь влиянием тока смещения. Если не учитывать этого обстоятельства, то H. ф. приводит к парадоксу, стремлению флуктуации к бесконечности при разрыве цепи (R ). Учёт влияния тока смещения изменяет H. ф. и снимает этот парадокс.

H. ф. является частным случаем общей теории эл.-магн. флуктуации (см. Флуктуации), к-рая основана на ур-ниях Максвелла с источником случайного шума, подобных ур-нию Ланжевена в теории броуновского движения.

Лит.: Ландау Л. Д., Лифшиц E. M., Электродинамика сплошных сред, 2 изд., M., 1982, гл. 11; Левин M. Л., Рытов С. M., Теория равновесных тепловых флуктуации в электродинамике, M., 1967, гл. 6; Введение в статистическую радиофизику, ч. 1 - Pытов С. M., Случайные процессы, M., 1976; Лифшиц E. M., Питаевский Л. П., Статистическая физика, ч. 2, M., 1978, гл. 8. Д. H. Зубарев.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.