ВЫРОЖДЕННОЕ ЭЛЛИПТИЧЕСКОЕ УРАВНЕНИЕ

- дифференциальное уравнение с частными производными

где действительная функция удовлетворяет условиям:

для всех действительных и существует 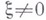, при к-ром в соотношении (2) достигается равенство. Здесь: хесть n-мерный вектор ; 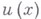-искомая функция, 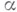- мультииндекс - вектор с компонентами

причем в уравнение (1) входят производные порядка не выше 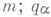- компоненты вектора есть n-мерный вектор Если в соотношении (2) для к.-л. х и Du идля всех действительных выполняется строгое неравенство, то уравнение (1) в точке 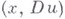является эллиптическим. Уравнение (1) вырождается в тех точках , где соотношение (2) обращается в равенство для к.-л. действительного . Если равенство достигается лишь на границе рассматриваемой области, то уравнение наз. вырождающимся на границе области. Наиболее исследованы линейные В. э. у. 2-го порядка

где матрица неотрицательно определенная для всех рассматриваемых значений х.

См. также ст. Вырожденное уравнение с частными производными н лит. при ней. А. М. Ильин.