ВЕТВЯЩИХСЯ ПРОЦЕССОВ РЕГУЛЯРНОСТЬ

- свойство ветвящегося процесса, обеспечивающее конечность числа частиц в любой момент времени. Вопрос о В. п. р. сводится, как правило, к вопросу о единственности решения нек-рого дифференциального или интегрального уравнения. Напр., в ветвящемся процессе с непрерывным временем дифференциальное уравнение

с начальным условием имеет единственное решение тогда и только тогда, когда при любом 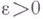расходится интеграл

В ветвящемся Беллмана-Харриса процессе производящая функция числа частиц есть решение нелинейного интегрального уравнения

где - функция распределения времени жизни частиц, 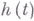- производящая функция числа непосредственных потомков одной частицы. Если при некоторых и целом для всех выполняются неравенства

го единственность решения уравнения (*) имеет место тогда и только тогда, когда уравнение

с начальными условиями

имеет единственное решение

Для регулярности ветвящегося процесса, описываемого уравнением (*), необходимо и достаточно, чтобы при любом интеграл

расходился.

Лит.:[1] Севастьянов Б. А., Ветвящиеся процессы, М., 1971. Б. А. Севастьянов.