- ВЕС
представления р алгебры Ли в векторном пространстве - отображение
алгебры Ли Lв ее поле определения k, для к-рого существует такой ненулевой вектор хпространства V, что
для всех
и некоторого целого 
(вообще говоря, зависящего от хи h), где 1 обозначает тождественное преобразование F. В этом случае говорят также, что 
- вес L-модуля V, определяемого представлением 
. Множество всех векторов 
, удовлетворяющих указанному условию, вместе с нулем образует подпространство 
, наз. весовым подпространством веса 
(или, соответствующим весу 
). Если 
, то Vназ. в е-совым пространством, или весовым модулем над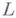 
, веса 
.
Если
- конечномерный весовой модуль над Lвеса 
, то контрагредиентный модуль (см. Контрагре-диентное представление) 
является весовым веса -
; если V и W - весовые модули над Lвесов 
соответственно, то их тензорное произведение 
является весовым модулем веса 
. Если L - ниль-потентная алгебра Ли, то весовое подпространство Va веса 
является подмодулем L-модуля V. Если, кроме того, 
, а 
- расщепляемая алгебра Ли линейных преобразований модуля V, то V разлагается в прямую сумму конечного числа весовых L-подмодулей разных весов:
(весовое разложение F относительно L). Если L - нильпотентная подалгебра конечномерной алгебры Ли M, рассматриваемой как L-модуль относительно присоединенного представления
алгебры М, и 
является расщепляемой алгеброй Ли линейных преобразований М, то соответствующее весовое разложение Мотносительно L:.
наз. разложением Фиттинга Мотносительно L, веса
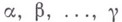наз. корнями, а пространства 
- корневыми подпространствами Мотносительно L. Если, кроме того, задано представление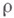 
алгебры Мв конечномерном векторном пространстве V, для которого 
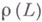- расщепляемая алгебра Ли линейных преобразований V, и
- соответствующее весовое разложение Vотносительно L, то
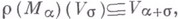когда 
есть вес Vотносительно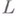 
, и 
=0 в противном случае. В частности, если 
- корень, то 
в остальных случаях 
. Если характеристика поля kравна нулю, то веса 
и корни 
, 
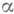являются линейными функциями на L, обращающимися в нуль на коммутанте алгебры L.
Лит.:[1] Джекобсон Н., Алгебры Ли, пер. с англ., М., 1964; [2] Желобенко Д. П., Компактные группы Ли и их представления, М., 1970. В, Л. Попов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
