- ВЕРХНИЙ И НИЖНИЙ ПРЕДЕЛЫ
- 1) В. и н. п. последовательности - наибольший, и соответственно, наименьший, предел среди всех частичных пределов (конечных и бесконечных) данной последовательности действительных чисел. Для любой последовательности действительных чисел
 множество всех ее частичных пределов (конечных и бесконечных) на расширенной числовой прямой (т. е. в множестве действительных чисел, пополненном символами
множество всех ее частичных пределов (конечных и бесконечных) на расширенной числовой прямой (т. е. в множестве действительных чисел, пополненном символами  ) не пусто и имеет как наибольший, так и наименьший элементы (конечный пли бесконечный). Наибольший элемент множества частичных пределов наз. верхним пределом (в. п.) последовательности и обозначается
) не пусто и имеет как наибольший, так и наименьший элементы (конечный пли бесконечный). Наибольший элемент множества частичных пределов наз. верхним пределом (в. п.) последовательности и обозначается
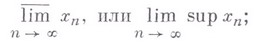
наименьший элемент - нижним пределом (н. п.) н обозначается

Напр., если
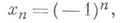
то

если
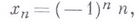
то

если
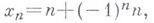
то
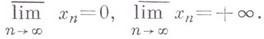
У всякой последовательности существует в. п. (н. п.), при этом, если последовательность ограничена cверху (снизу), то ее в. п. (н. п.) конечен. Для того чтобы число а было в. п. (соответственно н. п.) последовательности
 необходимо н достаточно, чтобы для любого
необходимо н достаточно, чтобы для любого  выполнялись условия: а) существует такой номер
выполнялись условия: а) существует такой номер  , что для всех номеров
, что для всех номеров  справедливо неравенство
справедливо неравенство  ; б) для любого номера пД существует такой номер
; б) для любого номера пД существует такой номер  , что
, что  Условие а) означает существование при любом фиксированном
Условие а) означает существование при любом фиксированном  в последовательности
в последовательности  лишь конечного числа таких членов
лишь конечного числа таких членов  , что
, что  . Условие б) означает существование бесконечного множества таких членов
. Условие б) означает существование бесконечного множества таких членов  , что
, что 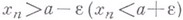 . Понятие н. п. сводится к понятию в. п. с помощью изменения знака у членов последовательности:
. Понятие н. п. сводится к понятию в. п. с помощью изменения знака у членов последовательности:

Для того чтобы последовательность
 имела предел (конечный или бесконечный, равный одному из символов
имела предел (конечный или бесконечный, равный одному из символов  ), необходимо и достаточно, чтобы
), необходимо и достаточно, чтобы

2) В. п. (н. п.) функции
 в точке
в точке  - предел верхних (нижних) граней множеств значений функции
- предел верхних (нижних) граней множеств значений функции  в окрестности точки
в окрестности точки  , когда эти окрестности стягиваются к точке
, когда эти окрестности стягиваются к точке 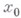 . Он обозначается
. Он обозначается

Пусть функция
 определена на метрич. пространстве
определена на метрич. пространстве  и принимает действительные значения на
и принимает действительные значения на  Если
Если 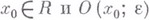 есть
есть  -окрестность точки
-окрестность точки  то
то

соответственно
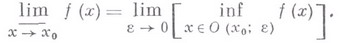
В каждой точке
 у функции
у функции  существуют как в. п.
существуют как в. п.  так и н. п.
так и н. п. 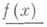 (конечные или бесконечные). Функция
(конечные или бесконечные). Функция 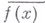 полунепрерывна сверху, а функция
полунепрерывна сверху, а функция  полунепрерывна снизу на пространстве
полунепрерывна снизу на пространстве  (в смысле понятия полунепрерывности функций, принимающих значения из расширенной числовой прямой).
(в смысле понятия полунепрерывности функций, принимающих значения из расширенной числовой прямой).
Для того чтобы функция
 в точке
в точке  имела предел, (конечный или бесконечный, равный одному из символов
имела предел, (конечный или бесконечный, равный одному из символов  ), необходимо п достаточно, чтобы
), необходимо п достаточно, чтобы

Естественным образом понятие в.. п. (н. п.) функции в точке переносится на действительные функции, определенные на топологич. пространствах.
3) В. п. (н. п.) последовательности множеств
 множество
множество

состоящее из таких элементов
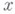 , к-рые принадлежат бесконечному числу множеств
, к-рые принадлежат бесконечному числу множеств  ; соответственно, множество
; соответственно, множество

таких элементов
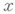 , к-рые принадлежат всем множествам
, к-рые принадлежат всем множествам  , начиная с нек-рого номера
, начиная с нек-рого номера  . Очевидно,
. Очевидно, 
Лит.:[1] Ильин В. А., Позняк Э. Г., Основы математического анализа, 3 изд., т. 1, М., 1971; [2] Колмогоров А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 4 изд., М., 1976; ГЗ] Кудрявцев Л. Д., Математический анализ, 2 изд., т. 1, М., 1973: [4] Никольский С. М., Курс математического анализа, т. 1, М., 1973; [5] Хаусдорф Ф., Теория множеств, пер. с нем., М., 1937. Л. Д. Кудрявцев.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
