ШУРА МУЛЬТИПЛИКАТОР

группы G - группа когомологий 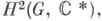где - мультипликативная группа комплексных чисел с тривиальным действием G. Ш. м. был введен И. Шуром [1] в связи с изучением конечномерных комплексных проективных представлений групп. Если - такое представление, то можно интерпретировать как отображение такое, что
где 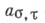- нек-рый коцикл со значениями в В частности, проективное представление 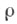является проективизацией нек-рого линейного представления тогда и только тогда, когда коцикл определяет нулевой элемент группы Если 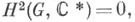то группа Gназ. замкнутой в смысле Шура. Если G- конечная группа, то существуют естественные изоморфизмы

Пусть 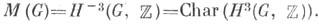Если задано центральное расширение

конечной группы G, то существует естественное отображение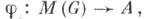 образ к-рого совпадает с 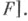Отображение совпадает с отображением 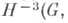индуцированным -произведением на 2-мерный коцикл из H²(G, А), определяющий расширение (*). Обратно, для любой подгруппы существует расширение (*) такое, что 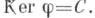Если G=[G, G], то расширение (*) однозначно определяется гомоморфизмом Если 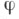- мономорфизм, то любое проективное представление группы G индуцируется нек-рым линейным представлением группы F.

Лит.:[1] Schur I., лJ. reine und angew. Math.