ШОТТКИ ТЕОРЕМА

если функция

регулярная аналитическая в круге D= {z : |z|<R} и не принимает в Dнек-рых конечных значений a₁, а ₂, то в любом круге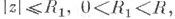 модуль |f(z)|ограничен числом M(a₁, a₂, c₀, R₁), зависящим только от a₁, a₂, c₀, R₁ (см. [1]). Более законченную формулировку получают, объединяя обобщенную Ш. т. и теорему Ландау при произвольном числе 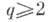выпускаемых значений. Пусть функция (*) не принимает нек-рых конечных значений 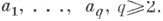Тогда, если 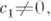то радиус R ограничен сверху числом, зависящим только от a₁, . . ., d_q, c₀, c₁ (теорема Ландау). Кроме того, в круге 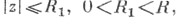модуль |f(z)| ограничен число 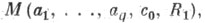зависящим только от a_l, . . ., a_q, c₀, R₁ (теорема Шоттки).
Геометрически Ш. т. означает, что сферич. расстояние (т. е. расстояние на Римана сфере )образа круга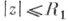 до точек а ₁, . . ., а _q не меньше числа d(а ₁, . . ., а _q, с₀, R₁), зависящего только от а ₁, . . ., а _q, с₀, R₁.Ш. т.- один из классич. результатов теории функций комплексного неременного типа искажения теорем.

Лит.:[1] Schottky F., лSitzungsber. Pfeuss. Akad. Wiss.