ЧЖОУ КОЛЬЦО

- кольцо классов алгебраических циклов на неособом квазипроективном алгебраич. многообразии относительно рациональной эквивалентности. Умножение в этом кольце определяется в терминах пересечения циклов (см. Пересечений теория).
Ч. к. многообразия Xявляется градуированным коммутативным кольцом, если обозначить через А ⁱ(X)группу классов циклов коразмерности i. При этом для морфизма гомоморфизм обратного образа является гомоморфизмом колец, а гомоморфизм прямого образа является (для собственных f) гомоморфизмом A(Y)-модулей. Последнее означает, что имеет место формула проекциий: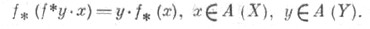

Ч. к. является областью значений для теории классов Чжэня алгебраич. расслоений (см. [1]), а именно, если Е - локально свободный пучок ранга г на многообразии X, Р (Е) - его проективизация, -канонич. проекция, -класс дивизоров, соответствующий обратимому пучку 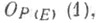то является вложением и Ч. к. (Р(Е))отождествляется с фактором кольца многочленов по идеалу, порожденному многочленом
Коэффициент наз. k-м классом Чжэня пучка Е.
В случае многообразий над полем комплексных чисел имеется гомоморфизм в кольцо сингулярных когомологии, удваивающий степени и совместимый с гомоморфизмами прямого и обратного образов.
Если X- особое квазипроективное многообразие, то его кольцо Чжоу (X)определяется как прямой предел колец: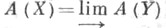 по всем морфизмам где Y неособо. Получается контра вариантный функтор в категорию градуированных колец, удовлетворяющий формуле проекций (см. [3]).

Лит.:[1] Хартсхорн Р., Алгебраическая геометрия, пер. с англ., М., 1981; [2] Anneaux de Chow et applications. Semlnaire Chevalley, P., 1958; [3] Fulton W., лPubl. Math. IHES