ФУРЬЕ - БЕССЕЛЯ РЯД — разложение функции f(x)в ряд где f(x) заданная в интервале (0, а)функция, Jv (х) Бесселя функция порядка положительные нули функции Jv(x), расположенные в порядке возрастания; коэффициенты ряда с т имеют следующие значения Если f(x) кусочно… … Математическая энциклопедия
БЕССЕЛЯ ФУНКЦИИ — цилиндрические функции1 го рода. Б. ф. .индекса рможет быть определена рядом сходящемся на всей плоскости. Б. ф. индекса рявляется решением соответствующего Бесселя уравнения. При действительных положительных значениях аргумента и индекса (… … Математическая энциклопедия
ФУРЬЕ РЯД — функции f(х)по ортонормированной на промежутке ( а, b )системе функций ряд коэффициенты к рого определяются по формулам и наз. коэффициентами Фурье функции f. О функции f в общем случае предполагается, что она интегрируема с квадратом на ( а, b) … Математическая энциклопедия
Фурье преобразование — Преобразование Фурье операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие … … Википедия
Преобразование Фурье — Преобразование Фурье операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие … … Википедия
ВЕСОВОЕ ПРОСТРАНСТВО — весовой класс, пространство с весом, пространство функций, имеющих конечную норму (или полунорму) с нек рым функциональным множителем весом. При этом норма (полунорма) функции наз. в этом случае весовой нормой (полунормой), х вес наз. также… … Математическая энциклопедия
Преобразование Лапласа — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются… … Википедия
Лапласа преобразование — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и … Википедия
Обратное преобразование Лапласа — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и … Википедия
Преобразование Радона — интегральное преобразование функции многих переменных, родственное преобразованию Фурье. Впервые введено в работе австрийского математика Иоганна Радона 1917 го года[1]. Важнейшее свойство преобразования Радона обратимость, то есть возможность… … Википедия
Г. Ганкель (Н. Hankel, 1875) установил теорему: если функция f(x)кусочно непрерывная и имеет ограниченную вариацию на любом интервале 0<х<l, интеграл 
В точках разрыва х 0,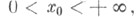
правая часть формулы (*) равна [f(x0 - 0)+f(x0 + 0)]/2, при x0 = 0 она дает f(0+)/2. Аналоги Ф. - Б. и. (*) для цилиндрич. функций Zv (х)других типов также справедливы, но пределы интегралов должны быть соответственно изменены. 