УСТОЙЧИВОСТЬ

в теории игр - принцип оптимальности, отражающий прямо или косвенно идею устойчивости ситуации (или множества ситуаций). Выделяют следующие основные концепции У.
1.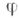 -устойчивость - см. Коалиционная игра.
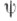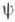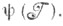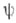2. -устойчивость - принцип оптимальности в кооперативных играх, связанный с понятием У. пары, состоящей из разбиения множества игроков Iна коалиции и дележа относительно образования новых коалиций. Разбиение множества игроков I наз. коалиционной структурой. Пусть <I, r> - кооперативная игра и -функция, сопоставляющая всякой коалиционной структуре множество коалиций Пара где х- дележ, наз. 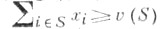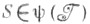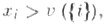-устойчивой, если для всех и когда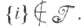
3. k-yстойчивость-частный случай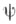 -устойчивости, когда в качестве 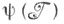берется множество коалиций, каждая из к-рых отличается от какою-либо элемента 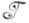не более чем на kигроков.
4. М-устойчивость - принцип оптимальности в теории кооперативных игр, формализующий интуитивное понимание У. образования коалиций и дележей значений v(Т)характеристич. функции vна образующихся коалициях Тмежду игроками из Тотносительно возможных угроз одних коалиций против других. Пара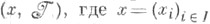 -вектор, удовлетворяющий условиям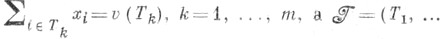 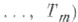- коалиционная структура, наз. конфигурацией. Конфигурация наз. индивидуально рациональной (и. р. к.), если 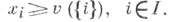Конфигурация 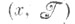наз. коалиционно рациональной (к. р. к.), если вектор худовлетворяет условию 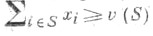для любой коалиции 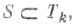k =1, ..., т. В случае, когда 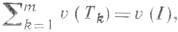в частности когда 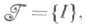для всякой и. р. к. 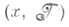вектор хявляется дележом.
Множество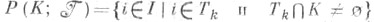 наз. множеством партнеров коалиции в коалиционной структуре 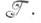Пусть 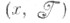-к. р. к. и 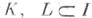-непересекающиеся коалиции. К. р. к. (y, U), удовлетворяющая условиям 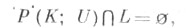y_i > x_i для всех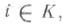 для всех 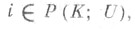наз. угрозой коалиции Кпротив L. Контругрозой коалиции . против Кназ. к. р. к. (z, V), удовлетворяющая условиям 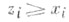для всех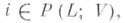 для всех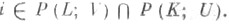
К. р. к.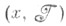 наз. M-устойчивой, если для любой пары непересекающихся коалиций К, L навсякую угрозу Кпротив L существует контругроза Lпротив К. Множество всех М-устойчивых конфигураций для коалиционной структуры 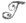наз. М-устойчивым множеством и обозначается через М или 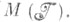В случае, когда 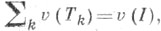множество Мсодержит с- ядро (см. Ядро в теории игр) кооперативной игры <I, v>. Множество Мчасто оказывается пустым, и поэтому чаще рассматривают множество к-рое определяется аналогично Мсо следующими изменениями: рассматриваются не только к. р. к., но и все и. р. к. и допускаются лишь угрозы и контругрозы между одноэлементными коалициями, т. е. между отдельными игроками. Было показано, что множество 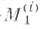не пусто для любой коалиционной структуры. Множество для содержит k- ядро и совпадает с ним и с-ядром для выпуклых игр<I, v>.
Понятия М- устойчивости и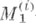 -устойчивости, имеют естественное обобщение на кооперативные игры без побочных платежей. Известно, что в этом случае множество 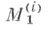может быть пустым; имеются нек-рые условия для непустоты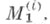

Лит.:[1] Aumann R. J., Мasсhlеr М,, в сб.: Advances in game theory, Princeton, 1964, p. 443-76; [2] Воробьев Н. Н., лУспехи матем. наук