ТРАНСПОРТНАЯ ЗАДАЧА

- один из наиболее важных частных случаев общей задачи линейного программирования. Содержательно Т. з. формулируется следующим образом.
Пусть в пунктах A₁, А₂, . . ., А _т производится нек-рый однородный продукт, причем объем производства лого продукта в пункте А _i составляет а _i единиц, i=1, . . ., т. Произведенный в пунктах производства продукт должен быть доставлен в пункты потребления B₁, В₂, . . ., В _n, причем объем потребления в пункте В _j составляет b_j единиц продукта. Предполагается, что транспортировка готовой продукции возможна из любого пункта производства в любой пункт потребления и транспортные издержки, приходящиеся на перевозку единицы продукта из пункта A_i в пункт B_j, составляют c_ij денежных единиц. Задача состоит в организации такого плана перевозок, при к-ром суммарные транспортные издержки были бы минимальными.
Формально задача ставится следующим образом. Пусть x_ij - количество продукта, перевозимого из пункта A_i в пункт B_j. Требуется определить совокупность из тп величин х _ij, удовлетворяющих условиям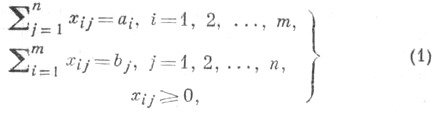

и обращающих в минимум линейную форму

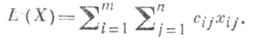
Группа ограничений (1) связана с тем обстоятельством, что объем вывезенного из каждого пункта производства продукта в точности равен объему произведенного в этом пункте продукта, а объем ввезенного в пункт потребления продукта в точности соответствует его потребности. При этих ограничениях необходимым и достаточным условием для разрешимости Т. з. является выполнение условия баланса

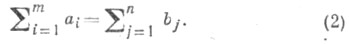
Специфическими для Т. з. являются следующие два обстоятельства: а) каждое из переменных x_ij входит в два уравнения системы (1); б) все коэффициенты при переменных x_ij принимают лишь два значения 0 или 1. Условия а) и б) позволили разработать для решения Т. з. алгоритмы, существенно более простые, чем симплексный метод, к-рый является одним из основных методов решения задач линейного программирования.
Наиболее известными из этих алгоритмов являются метод потенциалов и т. н. венгерский метод. Метод потенциалов - это метод последовательного улучшения плана (перевозок) с использованием второй теоремы двойственности для проверки оптимальности [1]. Венгерский метод - это метод последовательного построения допустимого плана, к-рый автоматически оказывается оптимальным. В основе венгерского алгоритма лежит метод чередующихся цепей [2].
Известны следующие два обобщения классич. Т. з., являющиеся отражением встречающихся на практике ситуаций. Открытая модель Т. э.- это Т. з. с нарушенным условием баланса (2), что означает либо превышение объема производства над объемом потребления, либо наоборот. Такая задача сводится к классич. Т. з. путем введения фиктивного пункта производства (или потребления) с мощностью производства (или потребления), равной разности объемов производства и потребления.
Много индексные транспортные задачи при сохранении общей проблемы минимизации транспортных издержек учитывают неоднородность груза (продуктов производства) и неоднородность транспортных средств.
За рубежом Т. з. иногда наз. проблемой Хичкока.

Лит.:[1] Гольштейн Е. Г., Юдин Д. В., Задачи линейного программирования транспортного типа, М., 1969; [2] Оре О., Теория графов, пер. с англ., М., 1968; [3] Емеличев В. А., Ковалев М. М., Кравцов М. К., Многогранники. Графы. Оптимизация, М., 1981.
В. К. Леонтьев.