ТРАНСЛЯТИВНОСТЬ МЕТОДА СУММИРОВАНИЯ

свойство метода, сохраняющее суммируемость ряда после добавления к нему или удаления из него конечного числа членов. Более точно: метод суммирования Аназ. транслятивным, если из суммируемости ряда

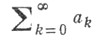
к сумме Sследует суммируемость этим же методом ряда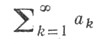

к сумме S-а₀, и наоборот. Для метода суммирования А, определенного преобразованием последовательности {S_n} в последовательность или функцию, свойство транслятивности состоит в том, что из условия A-limS_n = S следует А-limS_n+1 = S, и наоборот. Если метод суммирования определен регулярной матрицей то это означает, что из

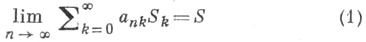
всегда следует

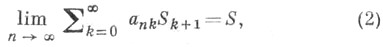
и наоборот. В случаях, когда такое заключение выполняется только в одну сторону, метод называют транслятивным справа - если из (1) следует (2), но обратное неверно, или транслятивным слева, когда из (2) следует (1), но обратное неверно.
Свойством транслятивности обладают многие распространенные методы суммирования; напр., метод Чезаро ( С, k )при k>0, метод Рисса (R, n, k) при k>0, метод Абеля транслятивны, экспоненциальный метод Бореля транслятивен слева.

Лит.:[1] Кук Р., Бесконечные матрицы и пространства последовательностей, пер. с англ., М., 1960; [2] Барон С., Введение в теорию суммируемости рядов, 2 изд., Таллин, 1977.
И. И. Волков.