ТОНКИЙ ПУЧОК

- пучок абелевых групп на паракомпактном пространстве X, пучок эндоморфизмов к-рого есть мягкий пучок. Пучок является Т. п. тогда и только тогда, когда для любых замкнутых подмножеств таких, что существует эндоморфизм 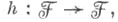тождественный над Аи равный 0 над В, или когда для любого открытого покрытия пространства Xсуществует такое локально конечное семейство эндоморфизмов пучка что supp и - тождественный эндоморфизм. Всякий Т. п. является мягким, а если - пучок колец с единицами, то верно и обратное. Если - Т. п., а - любой пучок абелевых групп на X, то - также Т. п. Примером Т. п. служит пучок ростков непрерывных (или дифференцируемых класса С ^k) сечений произвольного (соответственно дифференцируемого) векторного расслоения над паракомпактным пространством (соответственно паракомпактным дифференцируемым многообразием).

Лит.:[1] Годеман Р., Алгебраическая топология и теория пучков, пер. с франц., М., 1961; [2] Уэллс Р., Дифференциальное исчисление на комплексных многообразиях, пер. с англ., М., 1976.
А. Л. Онищик.