СУПЕРГРУППА

супергруппа Ли, - групповой объект в категории супермногообразий. С. задается функтором точек из категории коммутативных супералгебр в категорию групп. На С. переносятся Ли теоремы, что дает соответствие между С. и конечномерными супералгебрами Ли [1, 2].
Примеры. 1) С. задается функтором в группы четных обратимых матриц из M_n|m (С)(см. Суперпространство). т. е. матриц вида где X, Т- обратимые матрицы порядков п, т над a Y, Z - матрицы над Определен гомоморфизм заданный формулой

(березиниан);

2)С.

3) Подгруппы и оставляющие инвариантными четную или нечетную невырожденную симметрическую билинейную форму в соответствующем суперпространстве.
С каждой С. и ее подсупергруппой 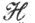связано супермногообразие представляемое функтором - однородное пространство С.

Лит.:[1] Березин Ф. А., Кац Г. И., лМатем. сб.