СТЬЮДЕНТА КРИТЕРИЙ

t - критерий,- значимости критерий для средних значений нормальных распределений.
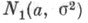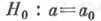Одновыборочный С. к. Пусть независимые случайные величины X₁, X₂, . . ., Х _п подчиняются нормальному закону, параметры к-рого аи неизвестны, и пусть проверяется сложная гипотеза против сложной альтернативы
Для решения этой задачи используется С. к., основанный на статистике

где

- оценки параметров аи вычисленные по выборке X₁, X₂, . . ., Х _п. При справедливости гипотезы H₀ статистика t_n-1 подчиняется Стъюдента распределению с f=n-1 степенями свободы, т. е.

где S_f(t) - функция распределения Стьюдента с f степенями свободы. Согласно одновыборочпому С. к. с уровнем значимости гипотезу H₀ следует принять, если

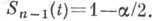где - квантиль уровня распределения Стьюдента с f= п-1 степенями свободы, т. е. - решение уравнения Напротив, если

то согласно С. к. уровня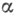 проверяемую гипотезу Н ₀ : а=а₀ следует отвергнуть и принять конкурирующую гипотезу
Двухвыборочпый С. к. Пусть X₁, X₂, . . ., Х _п и Y₁, Y₂, . . ., Y_m- взаимно независимые нормально распределенные случайные величины, имеющие одинаковую, но неизвестную дисперсию и пусть

причем параметры a₁ и a₂ тоже неизвестны (часто говорят, что имеются две независимые нормальные выборки). Далее, пусть проверяется гипотеза Н ₀ : а₁=а₂ против альтернативы В этом случае как проверяемая гипотеза Н ₀,так и конкурирующая гипотеза Н ₁ являются сложными. По наблюдениям X₁, X₂, . . ., Х _п и Y₁, Y₂, . . ., Y_m можно вычислить оценки

для неизвестных математич. ожиданий a_l и a₂, а также оценки

для неизвестной дисперсии Далее, пусть

Тогда при справедливости гипотезы Н ₀ статистика

подчиняется распределению Стьюдента с f=n+т-2 степенями свободы. Именно этот факт и лежит в основе двухвыборочного С. к., предназначенного для проверки Н ₀ против H₁. Согласно двухвыборочному С. к. уровня гипотеза H₀ принимается, если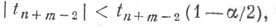

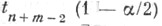где - квантиль уровня распределения Стьюдента с f=n+m-2 степенями свободы. Если же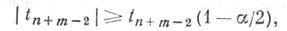

то согласно С. к. уровня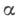 гипотеза Н ₀ отвергается в пользу Н ₁.

Лит.:[1]Крамер Г., Математические методы статистики, 2 изд., пер. с англ., М., 1975; [2] Уилкс С., Математическая статистика, пер. с англ., М., 1967; [3] Смирнов Н. В., Дунин-Барковский И. В., Краткий курс математич. статистики для технич. приложений, М., 1959; [4] Большев Л. Н., Смирнов Н. В., Таблицы математич. статистики, 3 изд., М., 1983; [5] Линник Ю. В., Метод наименьших квадратов и основы математико-статистич. теории обработки наблюдений, М., 1958.
М. С. Никулин.