АВТОМАТОВ ПОЛНЫЕ СИСТЕМЫ

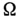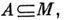специальные подмножества заданного класса Мавтоматов, на к-ром определено нек-рое множество операций со значениями в М. Эти подмножества обладают следующим основным свойством (свойством полноты): множество всех автоматов, к-рые получаются путем конечного числа применений операций из к автоматам из заданного подмножества совпадает с М. Задача о том, обладает ли множество свойством полноты или нет, наз. проблемой полноты (п. п.) для автоматов. Эта проблема изучена для различных моделей автоматов и операций. В порядке нарастания сложности объекта исследования сюда могут быть отнесены истинностные автоматы, автоматы, реализующие функции с задержками (т. е. функции k-значной логики с нек-рым временным сдвигом), конечные автоматы и др. П. п. для истинностных автоматов с обычно рассматриваемыми операциями суперпозиции по существу совпадает с п. п. для функций k-значной логики (см. Многозначная логика).и достаточно хорошо изучена. Под синхронной суперпозицией понимается такая суперпозиция автоматов, когда ко всем входам присоединяются автоматы, реализующие функции с одной и той же задержкой. Из найденных в этих случаях критериев полноты вытекает, в частности, существование алгоритма, устанавливающего для любой конечной системы автоматов ее полноту или неполноту. Основные критерии полноты даются в терминах так наз. предполных классов (т. е. таких подмножеств класса M, к-рые замкнуты относительно операций из 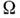и каждый из к-рых вместе с любым автоматом, ему не принадлежащим, образует полную систему). Показано, что множество Аявляется полным тогда и только тогда, когда оно не является подмножеством ни одного предполного класса, к-рые, в свою очередь, полностью описаны. Этот подход успешно осуществлен в целом ряде других случаев. Принципиально он возможен и при рассмотрении конечных автоматов, когда в качестве выбираются операции суперпозиции автоматов и операция обратной связи (см. Автоматов композиции). Здесь также справедлив указанный выше критерий, однако в этом случае установлено, что семейство предполных классов является континуальным, что исключает возможность получения эффективных критериев полноты в указанных терминах. Заметим, что во всех описанных случаях существуют конечные полные системы, и потому п. п. для произвольных систем автоматов сводится к п. п. для конечных систем автоматов. С последним обстоятельством, как и выше, связана задача об алгоритмич. разрешимости п. п. для конечных систем конечных автоматов. Эта проблема может быть обобщена: для данного автомата аи множества Втребуется определить, может ли абыть получен из автоматов множества Впри помощи заданного набора операций. Таким образом приходят к изучению предиката Р( х, у) -"автомат хреализуется набором у". Установлено, что проблема распознавания реализуемости алгоритмически неразрешима при любом фиксированном а, т. е. одноместный предикат Р( а, у).нерекурсивен. С другой стороны, при различных значениях Впараметра упредикат Р( х, В).может быть как рекурсивным, так и нерекурсивным. В связи с алгоритмич. неразрешимостью п. п. для автоматов возникает задача об отыскании классов множеств, для к-рых указанная проблема имеет эффективное решение. В частности, существует алгоритм для распознавания полноты систем, состоящих только из автоматов Мура и всех истинностных автоматов. С п. п. связана задача нахождения конкретных полных множеств автоматов с заданными свойствами. Установлено, что для любого натурального га существует полная система автоматов, никакая собственная подсистема к-рой не является полной, и таких систем при заданном n бесконечно много. Существует также в яек-ром смысле простейший автомат с двумя состояниями, двумя входными и одним выходным каналами, к-рый образует полную систему. П. п. рассматривается также для различных обобщений конечных автоматов и операций над ними; другое направление обобщений связано с введением различных отношений эквивалентности в рассматриваемом классе автоматов.

Лит.:[1] Яблонский С. В., "Тр. матем. ин-та АН СССР", 1958, т. 51, с. 5-142; [2] Кудрявцев В. В., "Проблемы кибернетики", 1962, в. 8, с. 91-115; [3] его же, там же, 1965, вып. 13, с. 45-74; [4] Кратко М. И., "Алгебра и логика. Тр. семинара", 1964, т. 3, № 2, с. 33-44; [51 Л е-тичевский А. А., Условия полноты в классе автоматов Мура, К., 1963; [6] Буевич В. А., "Проблемы кибернетики", 1970, в. 22, с. 75-83. В. Б. Кудрявцев.