СТИНРОДА КВАДРАТ

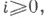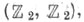- стационарная (стабильная) когомологическая операция Sqⁱ, типа повышающая размерность на i. Это означает, что для каждого натурального пи каждой пары топологич. пространств (X, Y) задан такой гомоморфизм что где - кограничный гомоморфизм (стационарность) и f*Sqⁱ - Sqⁱf^* для любого непрерывного отображения 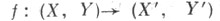(естественность). С. к. Sqⁱ обладает следующими свойствами:

1) Sq⁰=--id;
2) где - гомоморфизм Бокштейна, ассоциированный с короткой точной последовательностью групп коэффициентов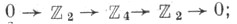
3) если i= dimx, то Sqⁱx=x²;
4) если i>dimx, то Sqⁱx=0;
5) (формула Картана)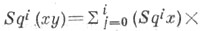
6) (соотношения Адема) при а<2bSq^a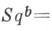 где 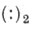- биномиальные коэффициенты mod 2.

В формуле Картана умножение можно считать как внешним ( -умножением), так и внутренним 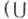-умножением). Она равносильна утверждению, что отображение 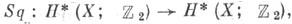определенное формулой

является гоморфизмом колец. Из условия стационарности вытекает, что С. к. Sqⁱ перестановочны с надстройкой и трансгрессией.
Операции Sqⁱ однозначно характеризуются свойствами 1), 3), 4), к-рые поэтому можно принять за определяющие их аксиомы. Конструктивное определение операций Sqⁱ основывается на симплициальной структуре в группах цепей C_*(X)и на существовании диагонального отображения Пусть W - минимальный ациклический свободный цепной -комплекс, т. е. цепной комплекс, для к-рого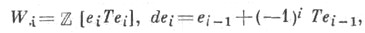

где Т - образующая группы Методом ацикличных носителей или явным построением (см. [4]) доказывается существование такого эквивариантного цепного отображения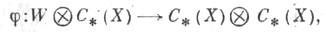

что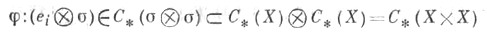

для любого симплекса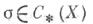 (символом 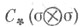здесь обозначен наименьший подкомплекс цепного комплекса содержащий элемент Пусть Любым двум коцепям ставится в соответствие формулой для любого симплекса 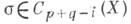коцепь наз. их -произведением. Для кограницы этой коцепи имеет место формула

из к-рой следует, что формула 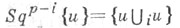корректно определяет нек-рый гомоморфизм

к-рый не зависит от выбора отображения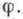
Аналогичным образом операции Sqⁱ строятся и в других симплициальных структурах с диагональным отображением, напр. в когомологиях симплициальных абелевых групп, симплициальных алгебр Ли и т. п. Однако при этом сохраняются не все свойства С. к. Sqⁱ (напр., вообще говоря, и единой общей теории обобщенных операций Sqⁱ до сих пор (1984) нет (см. [5], [6]).
Через С. к. и их аналоги при р>2 (см. Стинрода приведенная степень )выражаются многие когомологич. операции, действующие в группах когомологий с коэффициентами в группах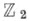 и , Это определяет основополагающую роль, к-рую С. к. играют в алгебраич. топологии и ее приложениях. Напр., группы бордизмов вычисляются с помощью С. к.
С. к. введен Н. Стинродом [4].

Лит.:[1] Стинрод Н., Эпстейн Д., Когомологические операции, пер. с англ., М., 1983; [2] Фукс Д. Б., Фоменко А. Т., ГутенмахерВ. Л., Гомотопическая топология, 2 изд., М., 1969; [3] Мошер Р. Э., Тангора М. К., Когомологические операции и их приложения в теории гомотопий, пер. с англ., М., 1970; [4] Stееnrоd N. Е., лAnn. Math.