СОВПАДЕНИЕ

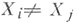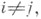связь,- группа наблюдений в выборке, имеющих равные значения. Пусть независимые случайные величины Х ₁,. . .. Х _п подчиняются одному и тому же абсолютно непрерывному вероятностному закону, плотность вероятности к-рого есть р(х). В таком случае, с вероятностью 1 среди наблюдений Х ₁, Х₂,. . ., Х _п не будет равных, т. е. если и, следовательно, каждый член Х (i) вариационного ряда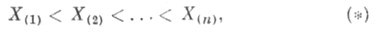

построенного по выборке Х ₁,. . ., Х _п, будет строго больше ему предшествующего X_(i-1).
Однако на практике в силу ошибок округлений при вычислении случайных величин Х ₁, . . ., Х _п могут появиться несколько групп наблюдений, в каждой из к-рых наблюдения равны между собой. Каждая такая группа совпавших наблюдений наз. совпадением. Таким образом, в общем случае вместо (*) экспериментатор может наблюдать вариационный ряд

где все 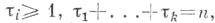вследствие чего, если присутствуют С., т. е. если существуют возникают трудности при определении вектора рангов, к-рый играет основную роль при построении ранговых статистик. Еще нет четких рекомендаций для определения рангов совпавших наблюдений. Наиболее распространены два подхода к решению этой задачи. Первый заключается в применении рандомизации. Согласно этому подходу в качестве рангов элементов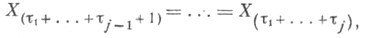

образующих j-ю группу, можно взять любую перестановку чисел

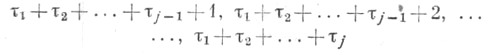
с вероятностью 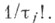Достоинство этого подхода заключается в его простоте, но при нек-рых альтернативах относительно закона распределения случайной величины Х _i на результатах статистич. выводов может сказаться примененная рандомизация.
При втором подходе рекомендуется всем совпавшим наблюдениям

образующим j-ю группу, приписать один и тот же т. н. средний ранг

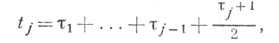
равный среднему арифметическому чисел 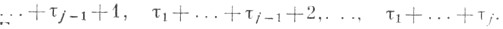Естественно, что такая процедура тоже сказывается на свойствах ранговых статистик, что следует учитывать на практике. Например, при построении статистики W Вилкоксона критерия при наличии С. рекомендуется пользоваться именно средними рангами, при этом математич. ожидание статистики Wостается таким же, как и в случае отсутствия С., а дисперсия DWуменьшается за счет усреднения рангов и становится равной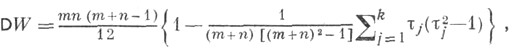

что следует учитывать при нормализации статистики W.

Лит.:[1] Гаек Я., Шидак 3., Теория ранговых критериев, пер. с англ., М., 1971; [2] Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, 2 изд., М., 1968.
М. С. Никулин.