- СВОБОДНОЕ ПРОИЗВЕДЕНИЕ
г р у п п Gi,
,- группа G, порожденная группами Gi, причем любые гомоморфизмы 
групп Gi в любую группу Нпродолжаются до гомоморфизма 
Для обозначения С. п. используется знак *, напр.:
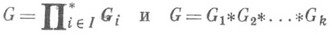
в случае конечного множества I. Каждый не равный единице элемент С. п. G единственным образом выражается в виде несократимого слова
, где 
, и при любом j=1,2, . . ., n-1, 
. Конструкция С. п. является важной в изучении групп, заданных множеством порождающих элементов и определяющих соотношений. В этих терминах оно может быть определено следующим образом. Пусть каждая группа Gi задана множествами Xi- порождающих и Ф i определяющих соотношений, причем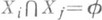 
, если 
. Тогда группа G,заданная множеством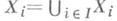 
порождающих и множеством Ф 
определяющих соотношений, будет С. п. групп 
.
Всякая подгруппа С. п. Gсама разлагается в С. п. своих подгрупп, из к-рых нек-рые являются бесконечными циклическими, а каждая из других сопряжена с нек-рой подгруппой какой-либо группы Gi, входящей в свободное разложение группы G(теорема К у р о ш а).
Лит.:[1] К у р о ш А. Г., Теория групп, 3 изд., М., 1967; [2] М а г н у с В., К а р р а с А., С о л и т э р Д., Комбинаторная теория групп, пер. с англ., М., 1974.
А. Л. Шмелъкин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
