- РЕШЕТКА С ДОПОЛНЕНИЯМИ
решетка L с нулем 0 и единицей 1, в к-рой для любого элемента асуществует такой элемент b(наз. д о п о л н е н и е м э л е м е н т а а), что
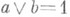 и
и 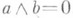 . Произвольную решетку можно вложить в решетку, каждый элемент к-рой обладает единственным дополнением. Если для любых
. Произвольную решетку можно вложить в решетку, каждый элемент к-рой обладает единственным дополнением. Если для любых 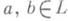 интервал[а, b]является Р. с д., то L наз. р е ш е т к о й с о т н о с и т е л ь н ы м и д о п о лн е н и я м и. Каждая модулярная Р. с д. является решеткой с относительными дополнениями. Решетка L с нулем 0 называется: а) р е ш е т к о й с ч а с т и чн ы м и д о п о л н е н и я м и, если каждый ее интервал вида [0, а],
интервал[а, b]является Р. с д., то L наз. р е ш е т к о й с о т н о с и т е л ь н ы м и д о п о лн е н и я м и. Каждая модулярная Р. с д. является решеткой с относительными дополнениями. Решетка L с нулем 0 называется: а) р е ш е т к о й с ч а с т и чн ы м и д о п о л н е н и я м и, если каждый ее интервал вида [0, а], , является Р. с д.; б) р е ш е т к о й с о с л а б ы м и д о п о л н е н и я м и, если для любых
, является Р. с д.; б) р е ш е т к о й с о с л а б ы м и д о п о л н е н и я м и, если для любых 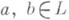 существует такой элемент
существует такой элемент  , что
, что 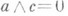 и
и  ; в) р е ш е т к о й с полудополнениями, если для любого
; в) р е ш е т к о й с полудополнениями, если для любого 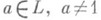 , существует такой элемент
, существует такой элемент  , что
, что  ; г) р е ш е т к о й с п с е в д о д о п о л н е н и я м и, если для любого
; г) р е ш е т к о й с п с е в д о д о п о л н е н и я м и, если для любого  существует такой элемент а*, что
существует такой элемент а*, что  тогда и только тогда, когда
тогда и только тогда, когда 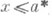 ; д) р е ш е т к о й с к в а з ид о п о л н е н и я м и, если для любого
; д) р е ш е т к о й с к в а з ид о п о л н е н и я м и, если для любого 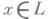 существует такой элемент
существует такой элемент  , что
, что 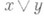 является плотным элементом. Большую роль играют также решетки с ортодополнениями (см. Ортомодулярная решетка). О связи между различными типами дополнений в решетках см. [4].
является плотным элементом. Большую роль играют также решетки с ортодополнениями (см. Ортомодулярная решетка). О связи между различными типами дополнений в решетках см. [4].
Лит.:[1] Б и р к г о ф Г., Теория структур, пер. с англ., М., 1952; [2] С к о р н я к о в Л. А., Элементы теории структур, 2 изд., М., 1982; [3] е г о ж е, Дедекиндовы структуры с дополнениями и регулярные кольца, М., 1961; [4] G r i 1 1 е t Р. А., V a r l e t J. С., "Bull. Soc. roy. Sci. Liege", 1967, t. 36, № 11 - 12, p. 628-42. Т. С. Фофанова.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
