РЕЛЯТИВНАЯ ГЕОМЕТРИЯ

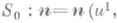
- геометрия конфигурации, состоящей из двух поверхностей и , находящихся в Петерсона соответствии. Аналогия между этим соответствием и сферическим отображением позволила ввести понятия релятивной площади, полной и средней кривизны и т. д., в частности релятивно минимальной поверхности (см. [1]).

Рассмотрение деривационных уравнений для репера

привело к понятию внутренней Р. г. поверхности S(см. [2]). Это есть геометрия аффинной связности (точнее эквиаффинной) без кручения. Было введено понятие геометрии 2-го рода, аналогичной геометрии сферич. отображения (см. [3]).

Р. г. позволяет включить в общую схему, кроме геометрии поверхностей евклидова и псевдоевклидова пространств, также и геометрию аффинной дифференциальной геометрии. Вектор 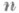аффинной нормали характеризуется тем, что асимптотич. сеть поверхности S - чебышевская (см. [3]).

Дальнейшим обобщением Р. г. является теория н о р м а л и з о в а н н ы х п о в е р х н о с т е й (см. [4]). С каждой точкой поверхности Sпроективного пространства связываются две прямые: нормаль 1-го рода, проходящая через точку поверхности А, но не имеющая с касательной плоскостью a других общих точек и нормаль 2-го рода, принадлежащая a, но не проходящая через А. На поверхности S определяются при этом две внутренние геометрии, сопряженные относительно асимптотич. сети. Построения Р. г. допускают многомерное обобщение (см. [4]).

Лит.:[1] М и 1 1 е r Е., "Monatsh. Math, und Physik", 1921, Bd 31, S. 3-19; [2] N о r d e n A. P. (H о р д е н А. П.), "С. г. Acad. sci.", 1931, t. 192, p. 135-37; [3] е г о ж е,"Изв. ВУЗов. Математика", 1958, № 4, с. 172-83; [4] е г о ж е, Пространства аффинной связности, 2 изд., М., 1976. А. П. Норден.