БИКОМПАКТНО ОТКРЫТАЯ ТОПОЛОГИЯ

одна из топологий на множестве отображений одного топо-логич. пространства в другое. Если F - некоторое множество отображений топология, пространства Xв то-пологич. пространство Y, то каждый конечный набор пар 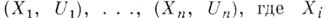- бикомпактное подмножество пространства - открытое подмножество пространства определяет подмножество тех отображений для к-рых одновременно 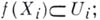совокупность всех таких подмножеств объявляется базой Б. <о. <т. на множестве F. Важность Б. <о. <т. следует из того,.что она входит существенным элементом в принадлежащую Л. С. Понтрягину теорию двойственности локально бикомпактных коммутативных групп и участвует в построении косых произведений. Если Y - хаусдорфoво пространство, то и Б. <о. <т. также удовлетворяет аксиоме отделимости Хаусдорфа. Если все отображения 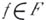непрерывны, а У- вполне регулярное пространство, то и множество F, наделенное Б. <о. <т., вполне регулярно. В предположении, что все отображения f непрерывны, а пространство Xлокаль-до..бикомпактно, Б. <о. <т. на Fявляется допустимой или .совместно непрерывной, т. е. отображение 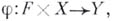..определяемое формулой 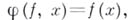непрерывно и при этом Б. <о. <т. является наименьшей (самой слабой) из всех топологий на F, для которых отображение ф . непрерывно. В этом преимущество Б. <о. <т. перед топологией поточечной сходимости, к-рая обычно слабее Б. <о. <т. и тогда она не является допустимой. Фундаментальное значение имеет и тот факт, что группа гомеоморфизмов бикомпакта Xна себя, наделенная Б. <о. <т., . является топологич. группой, непрерывно действующей (в смысле сказанного выше) на X. Группа гомеоморфизмов произвольного локально бикомпактного пространства на себя уже может не быть топологич. группой относительно Б. <о. <т. (переход к обратному элементу может оказаться разрывным отображением относительно этой топологии), но если локально бикомпактное пространство Xлокально связно, то снова Б. <о. <т. превращает группу всех гомеоморфизмов Xна себя в тонологич. группу, непрерывно действующую на X. Этот результат важен, ибо все многообразия локально бикомпактны и локально связны.

Лит.:[1 ] Келли Дж. Л., Общая топология, пер. с англ., М., 1968; [2] Понтрягин Л. С., Непрерывные группы, 2 изд., М., 1954; [3] Стинро Д Н., Топология косых произведений, пер. с англ., М., 1953; [4] Аrеns R., "Amer. J. Math.", 1946, v. 68, № 4, p. 593-610.

A. В. Архангельский, С. И. Сирота.