РАССЛОЕННОЕ ПРОИЗВЕДЕНИЕ

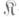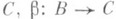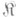о б ъ е к т о в к а т е г о р и и - частный случай понятия (обратного или проективного) предела. Пусть - произвольная категория и пусть заданы морфизмы из . Объект D, вместе с морфизмамй , наз. р а с с л о е н н ы м п р о и з в е д е н и е м о б ъ е к т о в А и В (над a. и b), если ja=yb и для любой пары морфизмов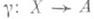

, для которой ga=db, существует такой единственный морфизм , что 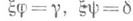Коммутативный квадрат

часто наз. у н и в е р с а л ь н ы м, и л и д е к а р т ов ы м, к в а д р а т о м. Объект Dвместе с морфизмами j и y есть предел диаграммы

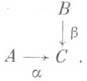
Р. п. объектов Аи Внад a и b обозначают одним из следующих способов:

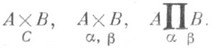
Р. п., если оно существует, определено однозначно с точностью до изоморфизма.

В категории с конечными произведениями и ядрами пар морфизмов Р. п. объектов Аи Внад a и b строится следующим образом. Пусть 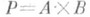-произведение Аи Вс проекциями p₁. и p₂ и пусть (D,m) - ядро пары морфизмов . Тогда D,вместе с морфизмамй mp₁=j и mp₂=y, есть Р. п. Аи Внад a и b. Во многих категориях структуризованных множеств Dявляется подмножеством произведения 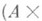, состоящим из всех таких пар ( а, b), где 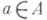, , для к-рых . М. Ш. Цаленко.