- РАСПРЕДЕЛЕНИЕ СТЕПЕННЫХ ВЫЧЕТОВ И НЕВЫЧЕТОВ
- распределение среди чисел 1, 2,. . ., т-1 тех значений х, для к-рых сравнение

n>1 - целое, разрешимо (неразрешимо). В вопросах, связанных с Р. с. в. и н., наиболее полно изучен случай простого модуля р. Пусть q=( п, р -1). Тогда сравнение yn=x(mod р). разрешимо при
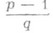 значениях хиз множества 1, 2, ... , р-1 и неразрешимо при остальных
значениях хиз множества 1, 2, ... , р-1 и неразрешимо при остальных 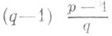 значениях х(см. Двучленное сравнение).
значениях х(см. Двучленное сравнение).
Однако сравнительно немного известно о том, как расположены эти значения среди чисел 1, 2,. . ., р-1.
Первые результаты о распределении степенных вычетов были получены еще К. Гауссом (С. Gauss, см. [1]) в 1706. С того времени и до работ И. М. Виноградова в вопросах о Р. с. в. и н. были получены лишь отдельные частные результаты. В 1915 И. М. Виноградов (см. [2]) доказал ряд общих результатов о распределении степенных вычетов и невычетов, а также первообразных корней но модулю рсреди чисел 1, 2,. . ., р. В частности, им была получена оценка
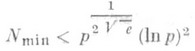
для наименьшего квадратичного невычета Nmin и оценка

где k - число различных простых делителей р-1, для наименьшего первообразного корня
 по простому модулю р. Кроме того, И. М. Виноградовым был высказан ряд гипотез о распределении квадратичных вычетов и невычетов (см. Виноградова гипотезы), стимулировавших ряд исследований в этой области. Так, Ю. В. Линник [3] доказал, что при достаточно большом Nна отрезке [Ne , N] количество простых чисел р, для к-рых Nmin>pe, не превосходит нек-рой константы С(e), зависящей лишь от e>0. Таким образом, простые числа р, для к-рых Nmin>pe , если только они существуют, встречаются очень редко. Другим существенным шагом в исследовании гипотез Виноградова явилась теорема Д. Бёрджесса [4]: для любого фиксированного сколь угодно малого
по простому модулю р. Кроме того, И. М. Виноградовым был высказан ряд гипотез о распределении квадратичных вычетов и невычетов (см. Виноградова гипотезы), стимулировавших ряд исследований в этой области. Так, Ю. В. Линник [3] доказал, что при достаточно большом Nна отрезке [Ne , N] количество простых чисел р, для к-рых Nmin>pe, не превосходит нек-рой константы С(e), зависящей лишь от e>0. Таким образом, простые числа р, для к-рых Nmin>pe , если только они существуют, встречаются очень редко. Другим существенным шагом в исследовании гипотез Виноградова явилась теорема Д. Бёрджесса [4]: для любого фиксированного сколь угодно малого 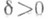 максимальное расстояние d(p).между соседними квадратичными невычетами удовлетворяет неравенству
максимальное расстояние d(p).между соседними квадратичными невычетами удовлетворяет неравенству

Отсюда, в частности, следует оценка
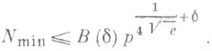
В этих неравенствах константы
 ,
, 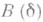 зависят только от
зависят только от 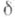 и не зависят от р. Доказательство теоремы Бёрджесса, сложное само по себе, основывалось на теореме Хассе - Вейля о числе решений гиперэллиптич. сравнения
и не зависят от р. Доказательство теоремы Бёрджесса, сложное само по себе, основывалось на теореме Хассе - Вейля о числе решений гиперэллиптич. сравнения  доказательство к-рой требовало привлечения аппарата абстрактной алгебраич. геометрии. Простой вывод теоремы Бёрджесса см. в [5], [6].
доказательство к-рой требовало привлечения аппарата абстрактной алгебраич. геометрии. Простой вывод теоремы Бёрджесса см. в [5], [6].
Лит.:[1] Г а у с с К. Ф., Труды по теории чисел, пер. с нем., М., 1959; [2] В и н о г р а д о в И. М., Избранные труды, М., 1952; 13] Л и н н и к Ю. В., "Докл. АН СССР", 1942, т. 36, с. 131; [4] B e r d g e s s D., "Mathematika", 1957, v. 4, № 8, p. 106-12; [5] С т е п а н о в С. А., "Тр. Матем. ин-та АН СССР", 1973, т. 132, с. 237 - 46; [6] К а р а ц у б а А. А., "Докл. АН СССР", 1968, т. 180, № 6, с. 1287-89. С. А. Степанов.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
