- ПОТОК
- понятие интуиционистской математики (см. Интуиционизм);совокупность, вид, состоящий из конечных кортежей натуральных чисел, называемых узлами П. (или допустимыми кортежами П.). Точнее, вид П кортежей натуральных чисел наз. потоком, если выполняются следующие условия: 1) существует эффективное правило а(т. н. закон потока), согласно к-рому для всякого кортежа <n1, ... , п т> можно выяснить, является ли он узлом П; 2) пустой кортеж < > является узлом всякого П.; 3) если кортеж <n1, ... , п т> есть узел П, то всякий его начальный кортеж вида <n1 ,... , ni> при
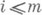также является узлом П; 4) если кортеж <nl ,... , nm> есть узел П, то найдется натуральное k такое, что <n1, ... , п т, k> есть узел П.Если кортежи натуральных чисел упорядочить, считая, что t<p тогда и только тогда, когда t есть собственное начало p, то с точки зрения этого порядка поток П представляет собой бесконечное дерево с началом < >, заданное эффективным образом (заданное законом). Свободно становящаяся последовательность a (или, более общо, произвольная эффективная функция, перерабатывающая натуральные числа в натуральные) наз. элементом потока П, символически
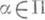, если для всякого пкортеж <a(0), ... , a(n-1)> является узлом П. В приложениях встречается также понятие оснащенного П. <Оснащенный поток Г состоит из потока П и эффективного правила Г п (т. н. дополнительного закона П.), приписывающего каждому узлу p потока П пек-рый объект Г п(p). Каждому элементу потока П при этом естественным образом соответствует последовательность объектов, задаваемых законом Г п.
В языке формального интуиционистского математич. анализа П. задается функцией - своим законом П. С этой целью рассматривается стандартное примитивно рекурсивное взаимно однозначное соответствие между кортежами натуральных чисел и натуральными числами. Пусть при этом кортежу < > соответствует О, операция соединения двух кортежей в один задается на их номерах примитивно рекурсивной функцией
означает номер кортежа с единственным членом х. Утверждение, что кортеж с номером хявляется узлом П., задаваемого a, записывается в виде а(х)=0. Тогда формула Spr(a), выражающая понятие "функция азадает П.", записывается в виде
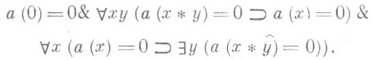
Наконец, если через
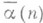обозначить номер кортежа <a(0), ... , a( п-1)>, где n - длина кортежа, то формула 
("a есть элемент П.,заданного а") записывается в виде 
В основаниях математики употребляются также обобщения понятия П., в к-рых используются кортежи не натуральных чисел, а более сложных объектов, напр. кортежи, составленные из свободно становящихся последовательностей.
Лит.:[1] Гейтинг А., Интуиционизм. Введение, пер. с англ., М., 1965. А. Г. Драгалин.
Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.
