ПОЛУРИМАНОВО ПРОСТРАНСТВО

пространство с полуримановой метрикой (с вырожденным метрич. тензором). П. п. является обобщением понятия риманова пространства. Определение П. п. может быть выражено с помощью понятий, применяемых при определении риманова пространства. В определении риманова пространства V_n используется в качестве касательного пространства евклидово пространство , причем касательные векторы в каждой точке инвариантны при параллельных переносах V _п (метрич. тензор a_ij пространства V_n абсолютно постоянен). Если в качестве касательного пространства в каждой точке пространства V _п берется полуевклидово пространство , то метрика пространства V _п будет являться вырожденной, метрич. тензор также абсолютно постоянен, но является теперь вырожденным, его матрица имеет ранг m₁ и имеет неособенную подматрицу. Определяется второй вырожденный метрич. тензор в ( п-m₁ )-плоскости (a_ijx^j = 0), к-рая наз. нулевой ( п-т ₁).плоскостью тензора а _ij; его матрица также обладает неособенной подматрицей и т. д. Последний, r-й метрич. тензор, определенный в нулевой ( п-m_r-1 )-плоскости (r-1)-го тензора,- невырожденный тензор с неособенной матрицей. Такое пространство и наз. П. п. и в этом случае обозначается символом . Аналогично определяется П. п. вида , т. <е. когда в качестве касательного пространства берется полупсевдоевклидово пространство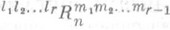

Пространства и наз. квазиримановыми пространствами.

Как и в римановом пространстве, в П. п. вводится понятие кривизны в двумерном направлении. Полугиперболич. и полуэллиптич. пространства являются П. п. постоянной ненулевой кривизны, а полуевклидово пространство - П. п. постоянной нулевой кривизны.

Таким образом, П. п. может быть определено как пространство аффинной связности (без кручения), касательные пространства к-рого в каждой точке являются полуевклидовыми (или полупсевдоевклидовыми), причем метрич. тензор П. п. является абсолютно постоянным.

В П. п. дифференциальная геометрия линий и поверхностей строится пв аналогии с дифференциальной геометрией линий и поверхностей в V_n с учетом указанной выше специфичности П. п. Поверхности полугиперболич. и полуэллиптич. пространств сами являются П. п. В частности, m-орисфера полугиперболич. пространства изометрична П. п. , метрика к-рого сводится к метрике полуэллиптич. пространства ; этот факт является обобщением изометричности орисферы пространства Лобачевского евклидовому пространству.

Лит.:[1] Розенфельд Б. А., Неевклидовы пространства, М., 1969. Л. А. Сидоров.