ПОКРЫТИЯ И УПАКОВКИ

- комбинаторные конфигурации, связанные с многозначным отображением одного множества на другое. Пусть заданы множества Vи Еи многозначное отображение Г множества Ена множество V. Пусть Г(е).- образ элемента 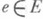при отображении Г и для любого 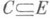пусть Г(С) =. Подмножество наз. покрытием (для (V, Е, Г)), если Г(С)=V. Подмножество наз. упаковкой, или укладкой (для (V, Е, Г)), если для любых двух различных элементов е _i, е _j из Рмножества Г( е _i). и Г(е _j) не пересекаются. Подмножество наз. совершенной упаковкой, или совершенным покрытием, если Рявляется одновременно и покрытием, и упаковкой. Множество Еназ. покрывающим, а множество V - покрываемым. Если обратное отображение Г ^-1 таково, что Г ^-1(V)=Е, то можно рассматривать V как покрывающее множество, а Екак покрываемое. Отображение 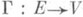определяет отношение инцидентности I, при к-ром v из Vи е из Еинцидентны (обозначение vIe), если .

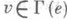С понятиями упаковки и покрытия связаны экстремальные задачи, заключающиеся в отыскании (по произвольно заданной тройке (V, Е, Г)) П. и у., доставляющих экстремум тех или иных функционалов. Такой функционал можно, напр., задать с помощью функции, сопоставляющей каждому элементу еиз Енеотрицательное действительное число w(e), наз. весом элемента е. Задача о минимальном покрытии заключается в построении покрытия С, для к-рого 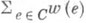принимает минимальное значение. Часто рассматривается случай, когда ; здесь речь идет о нахождении покрытия минимальной мощности, или т. н. кратчайшего покрытия. Если тройка (V, Е, Г) такова, что

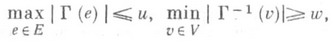
то минимальная мощность 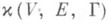покрытия удовлетворяет неравенствам

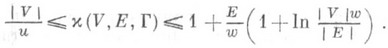
В экстремальных задачах об упаковках чаще всего требуется найти упаковки максимальной мощности. Иногда на покрываемом множестве Vзадается функция l, принимающая целые неотрицательные значения, тогда l-покрытием (l-упаковкой) наз. подмножество , удовлетворяющее условию: для каждого число s(v, Р).тех элементов , к-рые инцидентны элементу v, подчиняется неравенству 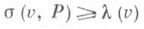(соответственно 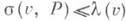). Существует связь между l-покрытиями минимальной мощности и l-упаковками максимальной мощности. Именно, пусть заданы множества Vи Е, многозначное отображение Г : Е V, а также функции l и l' на множестве Vтакие, что для каждого :

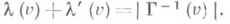
Тогда, если множество Сесть минимальное по мощности l-покрытие для (V, Е, Г), то множество Р= EС является максимальной по мощности l'-упаковкой, и наоборот: если Р- максимальная l'-упаковка, то множество С=ЕР. есть l-покрытие минимальной мощности. К классу задач о П. и у. относятся, напр., следующие:

1) Пусть G - граф с множеством вершин Vи множеством ребер Е. Если рассматривать множество Vв качестве покрываемого, множество Е - в качестве покрывающего и отношение инцидентности вершин и ребер - в качестве I, то покрытием является реберное покрытие графа, упаковкой - паросочетание, совершенной упаковкой - совершенное паросочетание. Если в качестве и покрывающего, и покрываемого взять множество вершин, а в качестве I - отношение смежности вершин, то покрытием будет внешне устойчивое множество, а упаковкой - внутренне устойчивое множество; при этом минимальная мощность покрытия наз. числом внешней устойчивости, а максимальная мощность упаковки - числом внутренней устойчивости (см. Графов числовые характеристики).

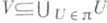2) Пусть V - непустое множество в метрич. пространстве R. Система л множеств наз. e-покрытием множества V, если диаметр d(U).любого множества не превосходит 2e и . Множество наз. e-сетью для множества V, если любая точка множества Vнаходится на расстоянии, не превышающем e, от нек-рой точки из S. Множество наз. e-различимым, если любые две его различные точки лежат на расстоянии, большем e. Пусть N_e (V) - минимальное число множеств в e-покрытии множества V, а М _e(V) - максимальное число точек в e-различимом подмножестве множества V. Число log₂N_e (V).наз. e-энтропией множества V, а log₂M_e( V).наз. e-емкостью множества V. Понятия e-энтропии и e-емкости применяются в теории приближения функций и в теории информации.

3) Пусть В ⁿ - единичный n-мерный куб с метрикой Хемминга и покрываемое множество есть множество его вершин, а покрывающее множество - множество шаров радиуса r в В ⁿ. Тогда множество центров шаров упаковки есть код, исправляющий rошибок. Если упаковка является совершенной, то код наз. плотно упакованным, или совершенным.

Если в качестве покрываемого множества взять подмножество N_f вершин куба В ⁿ, на к-ром нек-рая булева функция f( х ₁, . .., х _п).принимает значение 1, а в качестве покрывающего - множество граней (интервалов), целиком содержащихся в N_f, то покрытие наименьшей мощности будет соответствовать кратчайшей дизъюнктивной нормальной форме функции f(x₁,..., х _n), а покрытие с наименьшей суммой рангов - минимальной дизъюнктивной нормальной форме функции f(x₁ ,..., х _п).(см. Булевых функций нормальные формы).

В задачах о П. и у. оцениваются их мощности, исследуются вопросы существования, построения, перечисления совершенных упаковок, изучаются возможности построения эффективных алгоритмов для решения этих задач.

Лит.:[1] Роджерс К., Укладки и покрытия, пер. с англ., М., 1968; [2] Тот Л. Ф., Расположения на плоскости, на сфере и в пространстве, пер. с нем., М., 1958; [3] Питерсон У., Уэлдон Э., Коды, исправляющие ошибки, пер. с англ., М., 1976; [4] Дискретная математика и математические нопросы кибернетики, т. 1, М., 19.74; [5] Xарари Ф., Теория графов, пер. с англ., М., 1973; [6] Берж К., Теория графов и ее применения, пер. с франц., М., 1962; [7] Витушкин А. Г., Оценка сложности задачи табулирования, М., 1959; [8] Колмогоров А. Н., Тихомиров В. М., "Успехи матем. наук", 1959, т. 14, в. 2, с. 3-86; [9] Бахвалов Н. С., Численные методы, 2 изд., М., 1975; [10] Яблонский С. В., Введение в дискретную математику, М., 1979.

А. А. Сапоженко.